







二叉搜索树(BST)是一种特殊的二叉树,每个顶点最多可以有两个子节点。这种结构遵循BST属性,规定给定顶点的左子树中的每个顶点的值必须小于给定顶点的值,右子树中的每个顶点的值必须大于给定顶点的值。这个可视化实现了 'multiset' 属性:虽然所有的键都是不同的整数,但重复整数的信息被存储为频率属性(只显示出现多次的键)。作为演示,使用 函数来动画显示在上面随机生成的BST中搜索范围在1到99的随机值。
Adelson-Velskii Landis(AVL)树是一种自平衡的BST,它保持其高度在对数阶(O(log N)相对于AVL树中存在的顶点数(N)。
Remarks: By default, we show e-Lecture Mode for first time (or non logged-in) visitor.
If you are an NUS student and a repeat visitor, please login.
要在标准二叉搜索树和AVL树(主要在插入和删除整数时有所不同)之间切换,请选择相应的标题。
我们还提供一个URL快捷方式,可以快速访问AVL树模式,可在https://visualgo.net/en/avl找到。URL中的 'en' 可以替换为您首选语言的两个字符代码(如果有的话)。
Pro-tip 1: Since you are not logged-in, you may be a first time visitor (or not an NUS student) who are not aware of the following keyboard shortcuts to navigate this e-Lecture mode: [PageDown]/[PageUp] to go to the next/previous slide, respectively, (and if the drop-down box is highlighted, you can also use [→ or ↓/← or ↑] to do the same),and [Esc] to toggle between this e-Lecture mode and exploration mode.
BST,特别是像AVL树这样的平衡BST,是实现某种类型的表(或映射)抽象数据类型(ADT)的有效数据结构。
表ADT应该有效地支持至少以下三种操作:
- Search(v) — 确定v是否存在于ADT中,
- Insert(v) — 将v添加到ADT中,
- Remove(v) — 从ADT中删除v。
对于类似的讨论,请参考哈希表电子讲座幻灯片。
Pro-tip 2: We designed this visualization and this e-Lecture mode to look good on 1366x768 resolution or larger (typical modern laptop resolution in 2021). We recommend using Google Chrome to access VisuAlgo. Go to full screen mode (F11) to enjoy this setup. However, you can use zoom-in (Ctrl +) or zoom-out (Ctrl -) to calibrate this.
我们正在讨论一种特殊类型的表ADT,其中的键必须是有序的。这与允许无序键的其他类型的表ADT形成对比。
这种表ADT类型的具体要求将在后续幻灯片中进行阐明。
Pro-tip 3: Other than using the typical media UI at the bottom of the page, you can also control the animation playback using keyboard shortcuts (in Exploration Mode): Spacebar to play/pause/replay the animation, ←/→ to step the animation backwards/forwards, respectively, and -/+ to decrease/increase the animation speed, respectively.
使用未排序的数组或向量来实现表ADT可能会导致效率低下:
- Search(v)的时间复杂度为O(N),因为如果v不存在,我们可能需要遍历ADT的所有N个元素,
- Insert(v)可以用O(1)的时间复杂度实现,只需在数组的末尾追加v,
- Remove(v)的运行时间复杂度也为O(N),因为我们首先需要搜索v(已经是O(N)),然后关闭由删除操作产生的间隙 —— 这也是一个O(N)的操作。
用排序的数组或向量实现表ADT可以提高Search(v)的性能,但这是以牺牲Insert(v)性能为代价的:
- 现在可以用时间复杂度为O(log N)来实现Search(v),因为我们可以在排序的数组上使用二分查找策略,
- Insert(v)现在的操作时间复杂度为O(N),因为我们需要使用类似插入排序的策略来确保数组保持排序,
- Remove(v)仍然在O(N)时间复杂度下运行。虽然Search(v)在O(log N)下操作,但我们仍然需要关闭由删除引起的间隙,这在O(N)下运行。
本电子讲座的目标是介绍BST和平衡BST数据结构,即AVL树,它们使我们能够实现基本的表ADT操作,如 Search(v),Insert(v) 和 Remove(v) —— 以及其他一些表ADT操作(参见下一张幻灯片)——在O(log N) 时间内。这个时间复杂度明显小于 N。请尝试下面的交互式滑块,感受这个显著的差异。
log N = , N = .
PS: 更有经验的读者可能会注意到存在另一种数据结构,它可以更快地执行这三个基本的表ADT操作。但是,请继续阅读...
除了基本的三种操作外,还有几种其他的表ADT操作:
- 找到 Min()/Max() 元素,
- 找到 Successor(v),或者说是'下一个更大'的元素,和 Predecessor(v),或者说是'前一个更小'的元素,
- 按排序顺序列出元素,
- Rank(v) & Select(k),
- 还有其他可能的操作。
讨论:给定使用排序或未排序的数组/向量的约束,对于上述的前三个附加操作,最优的实现方式是什么?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
可用于实现表ADT的更简单的数据结构是链接列表。 Quiz: Can we perform all basic three Table ADT operations: Search(v)/Insert(v)/Remove(v) efficiently (read: faster than O(N)) using Linked List?
讨论:为什么?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
另一个可以用来实现表ADT的数据结构是哈希表。它具有非常快的 Search(v)、Insert(v) 和 Remove(v) 性能(所有这些都在预期的 O(1) 时间内)。
Quiz: So what is the point of learning this BST module if Hash Table can do the crucial Table ADT operations in unlikely-to-be-beaten expected O(1) time?
讨论上述答案!提示:回到前4张幻灯片。
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
我们现在将介绍BST数据结构。请参考上面提供的一个示例BST的可视化!
在BST中,根顶点是唯一的,没有父节点。相反,叶顶点,可以有几个,没有子节点。不是叶子的顶点被称为内部顶点。有时,根顶点不包括在内部顶点的定义中,因为只有一个顶点(即根顶点)的BST在技术上也可以符合叶子的定义。
在插图的例子中,顶点15是根,顶点5、7和50是叶子,顶点4、6、15(也是根)、23和71是内部顶点。
Each vertex has several key attributes: pointer to the left child, pointer to the right child, pointer to the parent vertex, key/value/data, and special for this visualization that implements 'multiset': frequency of each key (there are potential other attributes). Not all attributes will be used for all vertices, e.g., the leaf vertex will have both their left and right child attributes = NULL. Some other implementation separates key (for ordering of vertices in the BST) with the actual satellite data associated with the keys.
The left/right child of a vertex (except leaf) is drawn on the left/right and below of that vertex, respectively. The parent of a vertex (except root) is drawn above that vertex. The (integer) key of each vertex is drawn inside the circle that represent that vertex and if there are duplicated insertion of the same (integer) key, there will be an additional hyphen '-' and the actual frequency (≥ 2) of that key. In the example above, (key) 15 has 6 as its left child and 23 as its right child. Thus the parent of 6 (and 23) is 15. Some keys may have '-' (actual frequency) in random fashion.
Discussion: It is actually possible to omit the parent pointer from each vertex. How?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
在这个可视化中,我们允许重复的整数,通过保持N(整数)键的不同,但任何现有键的重复将被存储为该键的'frequency'属性(可视化为'-'(实际频率,但只有当它≥2时))。因此,我们可以使用简单的BST属性,如下:对于每个顶点X,X的左子树上的所有顶点都严格小于X,X的右子树上的所有顶点都严格大于X。
在上面的例子中,根15的左子树上的顶点:{4, 5, 6, 7}都小于15,根15的右子树上的顶点:{23, 50, 71}都大于15。你也可以递归地检查其他顶点的BST属性。
在这个可视化中,我们允许键在[-99..99]的范围内。
我们为以下常见的 BST/AVL 树操作提供可视化:
- 查询操作(BST 结构保持不变):
- Search(v)(或 LowerBound(v)),
- Predecessor(v)(以及类似的 Successor(v)),以及
- Inorder/Preorder/Postorder 遍历,
- 更新操作(BST 结构(很可能)会改变):
- 创建 BST(几个标准),
- Insert(v),以及
- Remove(v)。
在 VisuAlgo 中,还有一些其他的 BST (查询) 操作还未被可视化:
- Rank(v):给定一个键v,确定它在 BST 元素排序顺序中的排名(基于1的索引)。也就是说,Rank(FindMin()) = 1 和 Rank(FindMax()) = N。如果v不存在,我们可以报告 -1。
- Select(k):给定一个排名k,1 ≤ k ≤ N,确定在 BST 中具有该排名k的键v。或者换句话说,找到 BST 中第k小的元素。也就是说,Select(1) = FindMin() 和 Select(N) = FindMax()。
这两个操作的详细信息目前在某个 NUS 课程中被隐藏,以便于教学。
如果没有(或很少)更新,特别是插入和/或删除操作,那么这种数据结构就被称为静态 (static) 数据结构。
即使有很多更新操作,也能保持高效的数据结构被称为动态 (dynamic) 数据结构。二叉搜索树(BST)和特别是平衡二叉搜索树(例如,AVL树)属于这一类别。
由于数据(对于这个可视化来说是不同的整数)在BST中的组织方式,我们可以二分搜索一个整数v(这就是二叉搜索树的名字的由来)。
首先,我们将当前顶点设置为根,然后检查当前顶点是小于/等于/大于我们正在搜索的整数v。然后我们分别进入右子树/停止/进入左子树。我们一直这样做,直到我们找到所需的顶点或者我们找不到。
在上面的BST示例中,尝试点击 (在2次比较后找到),(在3次比较后找到),(在2次比较后未找到 - 在这一点上我们会意识到我们找不到21)。
请注意,这个术语是基于C++ std::set::lower_bound中给出的定义。其他编程语言,例如,Java TreeSet有一个类似的方法 "higher()"。
如果v存在于BST中,那么 lower_bound(v)与Search(v)相同。但是,如果v不存在于BST中,lower_bound(v)将找到BST中严格大于v的最小值(除非v > BST中的最大元素)。如果稍后将这个当前不存在的v插入到这个BST中,这就是它的位置。
同样,由于BST内部数据的组织方式,我们可以通过从根开始,分别向左/右子树不断前进,找到最小/最大元素(在这个可视化中是一个整数)。
尝试点击上面示例BST中的 和 。答案应该是4和71(分别在与从根到最左顶点/最右顶点的3个整数比较后得出)。
Search(v)/lower_bound(v)/SearchMin()/SearchMax() 操作在 O(h) 中运行,其中 h 是 BST 的高度。
但请注意,如上面的随机 '偏右' 示例所示,这个 h 在普通 BST 中可以高达 O(N)。尝试 (这个值不应该存在,因为我们只使用 [1..99] 之间的随机整数来生成这个随机 BST,因此 Search 程序应该从根检查到唯一的叶子,时间为 O(N) —— 效率不高。
- 如果 v 具有右子树,则 v 的右子树中的最小整数必须是 v 的后继。尝试(应为50)。
- 如果 v 没有右子树,我们需要遍历 v 的祖先,直到我们找到'右转'到顶点 w(或者,直到我们发现第一个大于顶点 v 的顶点 w)。 一旦我们找到顶点 w,我们将看到顶点 v 是 w 的左子树中的最大元素。 试试(应该是15)。
- 如果 v 是BST中的最大整数,则 v 没有后继。 试试(应该没有)。
尝试相同的三个镜像的极端情况:(应为5),(应为23),(应为无/none)。
此时,请暂停一会并思考这三个后继(v)/ 前驱(v)案例,以确保您理解这些概念。
但请记住,这个h可以和正常BST中的 O(N) 一样高,如上面的随机“倾斜右侧”示例所示。 如果我们调用,我们将在 O(N) 时间从最后一个叶子回到根 - 效率不高。
中序遍历是一种递归方法,我们首先访问左子树,遍历左子树中的所有项,访问当前子树的根,然后浏览右子树和右子树中的所有项。 不用多说了,让我们尝试,看看它在上面的BST示例中如何操作。
无论BST的高度如何,Inorder Traversal都以O(N)运行。
讨论:为什么?
PS:有些人调用N个无序整数插入O(N log N)中的BST,然后执行O(N)Inorder Traversal作为'BST sort'。 它很少使用,因为有几种比这更容易使用(基于比较)的排序算法。
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
我们已经包含了前序遍历和后序遍历树的动画方法。
基本上,在前序遍历中,我们在访问左子树和右子树之前先访问当前的根。对于背景中显示的示例BST,我们有:{{15},{6, 4, 5, 7},{23, 71, 50}}。
PS:你注意到递归模式了吗?根,根的左子树的成员,根的右子树的成员。
在后序遍历中,我们先访问左子树和右子树,然后再访问当前的根。对于背景中显示的示例BST,我们有:{{5, 4, 7, 6},{50, 71, 23},{15}}。
讨论:给定一个BST的前序遍历,例如[15, 6, 4, 5, 7, 23, 71, 50],你能用它恢复原始的BST吗?对于后序遍历的类似问题也是可能的。
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
我们可以通过执行类似于Search(v)的操作将新的整数插入到BST中。但是这次,我们不再报告新的整数未找到,而是在插入点创建一个新的顶点,并将新的整数放在那里。尝试在上面的例子中使用 (第一次插入将创建一个新的顶点,但请看下面)。
由于我们现在实现了 'multiset',我们可以插入重复的元素,例如,尝试在上面的例子中使用 (多次)或再次点击 (重复的)。
到目前为止你应该知道这个 h 在正常BST中可以和 O(N) 一样高,如上面随机的“向右倾斜”示例所示。 如果我们调用,即我们插入一个大于当前最大值的新整数,我们将在O(N)时间内从根向下移动到最后一个叶子,然后插入新整数作为最后一个叶子的右子节点 - 效率不高(请注意,在此可视化中我们最多只允许h=9)。
Quiz: Inserting integers [1,10,2,9,3,8,4,7,5,6] one by one in that order into an initially empty BST will result in a BST of height:
专业提示:您可以使用“探索模式”来验证答案。
我们可以通过执行类似于 Search(v) 的操作来从BST中删除一个整数。
如果在BST中找不到 v,我们就什么都不做。
如果在BST中找到了 v,我们不会报告找到了现有的整数 v,而是进行以下检查。如果 v 的频率 ≥ 2,我们只需将其频率减一,而不做任何其他操作。然而,如果 v 的频率正好为1,我们将执行三种可能的删除情况之一,这将在三个单独的幻灯片中详细说明(我们建议你逐一尝试它们)。
第一个情况是最简单的:顶点 v 目前是BST的叶子顶点之一。
删除叶子顶点非常简单:我们只需删除那个叶子顶点 - 尝试在上面的BST示例上点击 (如果随机化导致顶点5有多于一个的副本,只需再次点击该按钮)。
这部分显然是 O(1) ——在早先的 O(h) 搜索类似的努力之上。
第二种情况也不是那么难:顶点 v 是 BST 的(内部/根)顶点,并且它有 恰好一个子节点。如果不做任何其他操作就删除 v,将会断开 BST。
删除只有一个子节点的顶点并不难:我们将该顶点的唯一子节点与该顶点的父节点连接起来 - 尝试在上面的 BST 示例上点击 (如果随机化导致顶点 23 有多于一个的副本,只需再次点击该按钮)。
这部分也显然是 O(1) ——在早先的 O(h) 搜索类似的努力之上。
三个情况中,第三个情况是最复杂的:顶点 v 是BST的(内部/根)顶点,它有正好两个子节点。如果不做任何其他操作就删除 v,将会断开BST。
删除具有两个子节点的顶点的方法如下:我们用它的后继顶点替换该顶点,然后在其右子树中删除其重复的后继顶点 - 尝试在上面的示例BST上 (如果随机化导致顶点6有多于一个的副本,只需再次点击该按钮)。
由于需要找到后继顶点,这部分需要 O(h) —— 除了之前的 O(h) 搜索类似的努力。
本案例3值得进一步讨论:
- 为什么用后继C替换有两个子节点的顶点B总是一个有效的策略?
- 我们可以用它的前身A替换有两个子节点的顶点B吗? 为什么或者为什么不?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
Remove(v) 的运行时间为 O(h),其中 h 是 BST 的高度。删除情况 3(删除具有两个子节点的顶点是最“重”的,但它不超过 O(h))。
如您现在应该完全理解的,h 在正常的 BST 中可以像在上面的随机“偏右”示例中一样高达 O(N)。如果我们调用 ,即我们删除当前的最大整数,我们将从根节点下降到最后一个叶节点,然后在 O(N) 时间内删除它(当其频率为 1 时)——这并不高效。
To make life easier in 'Exploration Mode', you can create a new BST using these options:
- Empty BST (you can then insert a few integers one by one),
- A few e-Lecture Examples that you may have seen several times so far,
- Random BST (which is unlikely to be extremely tall — the expected height of a randomly built BST is still O(log N)),
- Skewed Left/Right BST (tall BST with N vertices and N-1 linked-list like edges, to showcase the worst case behavior of BST operations; disabled in AVL Tree mode).
We are midway through the explanation of this BST module. So far we notice that many basic Table ADT operations run in O(h) and h can be as tall as N-1 edges like the 'skewed left' example shown — inefficient :(...
So, is there a way to make our BSTs 'not that tall'?
PS: If you want to study how these basic BST operations are implemented in a real program, you can download this BSTDemo.cpp | py | java.
此时,我们建议您按 [Esc] 或单击此e-Lecture幻灯片右下角的X按钮进入“探索模式”并自行尝试各种BST操作,以加强您对这种多功能数据结构的理解。
当您准备继续阅读平衡BST(以AVL树为示例)时,再次按 [Esc] 或从右上角的下拉菜单中将模式切换回“电子演讲模式”。 然后,使用幻灯片选择器下拉列表this slide 12-1恢复。
我们将继续讨论平衡BST的概念,以使得 h = O(log N)。
我们专注于AVL Tree(Adelson-Velskii&Landis,1962),以其发明者Adelson-Velskii和Landis命名。
其他平衡的BST实现(或多或少好于常数因子c)是:红黑树,B树/ 2-3-4树(Bayer&McCreight,1972),Splay树(Sleator 和Tarjan,1985),Skip Lists(Pugh,1989),Treaps( Seidel和Aragon,1996)等。
对于每个顶点v,我们定义height(v):从顶点v到其最深叶子的路径上的边数。 此属性保存在每个顶点中,因此我们可以在O(1)中访问顶点的高度,而无需每次都重新计算它。
正式公式是:
v.height = -1 (if v is an empty tree)因此,BST的高度是: root.height。
v.height = max(v.left.height, v.right.height) + 1 (otherwise)
在上面的例子BST上, height(11) = height(32) = height(50) = height(72) = height(99) = 0 (所有都是叶子)。height(29) = 1,因为有1个边将它连接到它唯一的叶子32上。
Quiz: What are the values of height(20), height(65), and height(41) on the BST above?
height(20) = 2height(41) = 3
height(65) = 2
height(41) = 4
height(65) = 3
height(20) = 3
If we have N elements/items/keys in our BST, the lower bound height h = Ω(log2 N) (the detailed formula in the next slide) if we can somehow insert the N elements in perfect order so that the BST is perfectly balanced.
See the example shown above for N = 15 (a perfect BST which is rarely achievable in real life — try inserting any other (distinct) integer and it will not be perfect anymore).
N ≤ 1 + 2 + 4 + ... + 2h
N ≤ 20 + 21 + 22 + … + 2h
N ≤ 2h+1-1 (sum of geometric progression)
N+1 ≤ 2h+1 (apply +1 on both sides)
log2 (N+1) ≤ log2 2h+1 (apply log2 on both sides)
log2 (N+1) ≤ (h+1) * log2 2 (bring down the exponent)
log2 (N+1) ≤ h+1 (log2 2 is 1)
h+1 ≥ log2 (N+1) (flip the direction)
h ≥ log2 (N+1)-1 (apply -1 on both sides)
If we have N elements/items/keys in our BST, the upper bound height h = O(N) if we insert the elements in ascending order (to get skewed right BST as shown above).
The height of such BST is h = N-1, so we have h < N.
Discussion: Do you know how to get skewed left BST instead?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
那么,对于一个小的常数因子c,我们可以得到高度接近 log2 N 的BST,即高度c * log2 N 的 BST 吗? 如果可以,那么需要O(h)运行的BST操作实际上只需 O(log N) 运行...
在AVL树中,我们稍后会看到它的高度 h < 2 * log N(有更严谨的分析,但我们将在VisuAlgo中使用 c = 2 情况下的较简单的分析)。 因此,大多数AVL Tree操作以 O(log N) 时间高效运行。
插入(v)和删除(v)更新操作可能会更改AVL树的高度 h,但我们将看到旋转操作以保持较低的 AVL 树高度。
相反,我们在 Insert(v)/Remove(v) 操作的后面计算 O(1) 的:x.height = max(x.left.height, x.right.height) + 1,因为只有沿插入/移除路径的顶点的高度 (height) 可能会受到影响。 因此,只有 O(h) 顶点可以改变其 height(v) 属性,并且在AVL树中,h <2 * log N.
在示例AVL树上尝试(暂时忽略生成的旋转,我们将在接下来的几张幻灯片中回到它)。 请注意,沿插入路径只有几个顶点:{41,20,29,32}将高度增加+1,所有其他顶点的高度不变。
如果BST中的每个顶点都是高度平衡的,则根据上面的不变式此BST被称为高度平衡。 这样的BST称为AVL Tree,就像上面的例子一样。
在这里暂停一会,并尝试插入一些新的随机顶点或删除一些随机存在的顶点。 生成的BST是否仍然被认为是高度平衡的?
证明依赖于高度为 h 的最小 AVL 树。
令 Nh 为高度为h的AVL树中的最小顶点数。
Nh的前几个值是N0 = 1(单个根顶点),N1 = 2(只有一个左子或一个右子的根顶点),N2 = 4,N3 = 7,N4 = 12,N5 = 20(见背景图片),等等(见下两张幻灯片)。
我们知道,对于 N 个顶点的任何其他AVL树(不一定是最小尺寸的),N ≥ Nh。
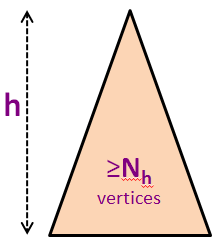
在背景图片中,我们有N5 = 20个顶点,但我们知道在我们有一个高度为h = 5的完美二叉树之前,我们可以再挤进43个顶点(最多N = 63)。
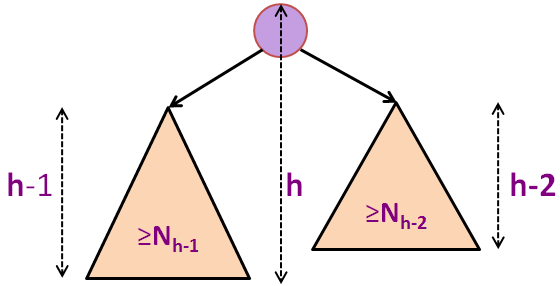
Nh = 1 + Nh-1 + Nh-2 (高度为h的最小大小AVL树的公式)
Nh > 1 + 2*Nh-2 (因为 Nh-1 > Nh-2)
Nh > 2*Nh-2 (显然)
Nh > 4*Nh-4 (递归)
Nh > 8*Nh-6 (另一步递归)
... (我们只能做这个h/2次,假设初始h是偶数)
Nh > 2h/2*N0 (我们达到基本情况)
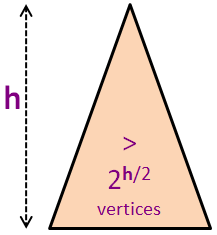
Nh > 2h/2 (因为 N0 = 1)
N ≥ Nh > 2h/2 (结合前两张幻灯片)
N > 2h/2
log2(N) > log2(2h/2) (两边都取 log2)
log2(N) > h/2 (公式简化)
2 * log2(N) > h 或 h < 2 * log2(N)
h = O(log(N)) (最终结论)
再看一下BST示例。 看到所有顶点都是高度平衡的AVL树。
为了快速检测顶点v是否高度平衡,我们将AVL树的(内部具有绝对函数的)不变式修改为:bf(v) = |v.left.height - v.right.height|。
现在再次在AVL树上尝试。 插入路径上的几个顶点:{41,20,29,32}的高度增加1。 在插入之后顶点{29,20}将不再高度平衡了(并且将在稍后旋转 - 在接下来的几张幻灯片中讨论),i.e. bf(29)= -2和bf(20)= -2。 我们需要恢复平衡。
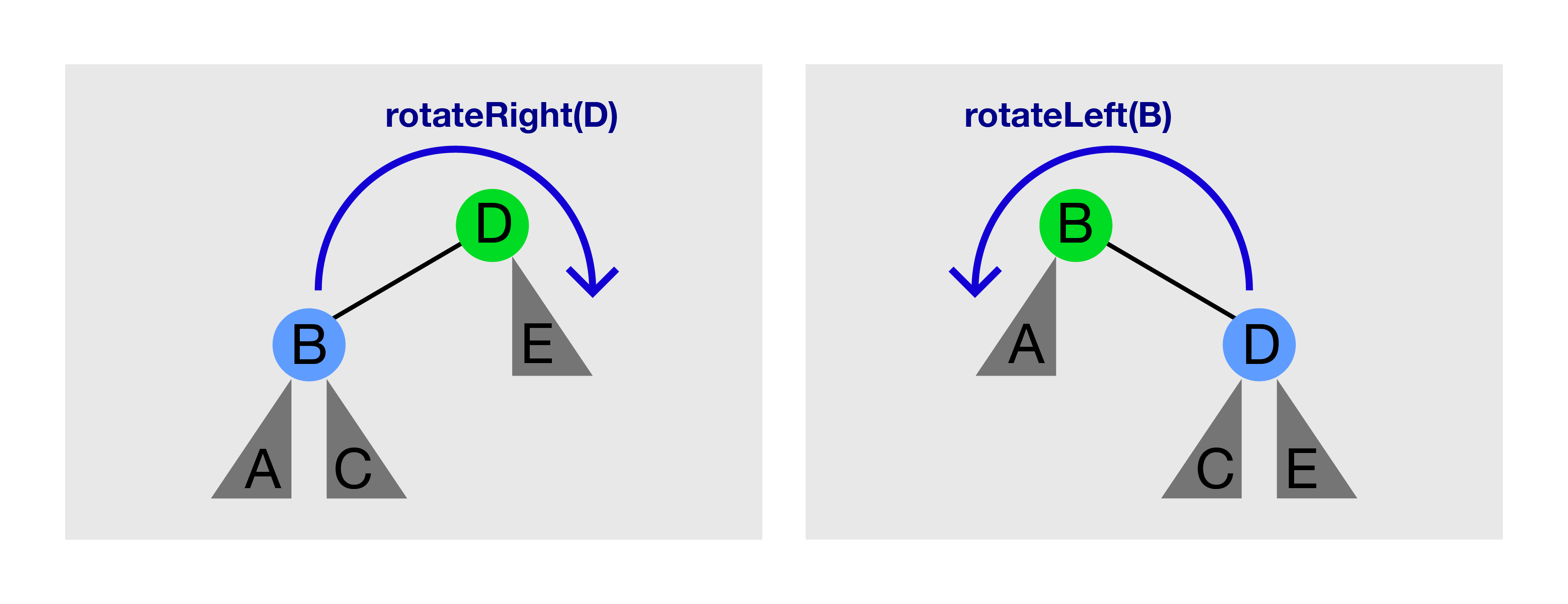
看上面的图片。在左图上调用 rotateRight(D) 将产生右图。在右图上调用 rotateLeft(B) 将再次产生左图。
只有当 T 有左/右子节点时,才能调用 rotateRight(T)/rotateLeft(T)。
树旋转 保留 BST 属性。
旋转前,A < B < C < D < E。
旋转后,注意以 C 为根的子树(如果存在)更换了父节点,
但 A < B < C < D < E 的顺序并未改变。
BSTVertex rotateLeft(BSTVertex T) // 先决条件:T的右子节点 T.right != null
BSTVertex w = T.right // 右旋是这个的镜像
w.parent = T.parent // 这个方法新手很难写对
T.parent = w
T.right = w.left
if (w.left != null) w.left.parent = T
w.left = T
// 更新 T 和 w 的高度 height
return w
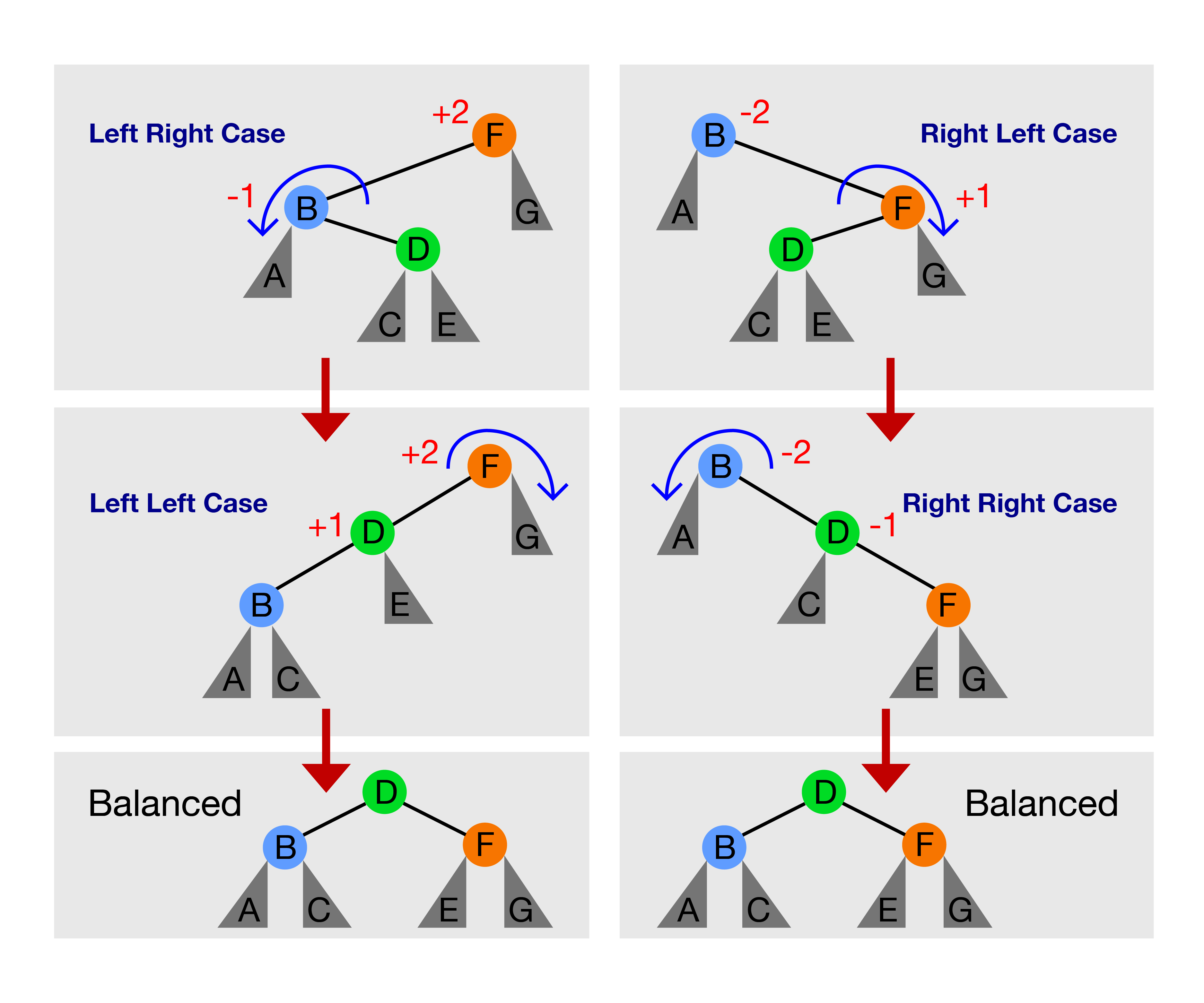
只有以下四种情况:
- 左左情况:bf(F) = +2 和 bf(D) = +1,解决方案:rotateRight(F)
- 左右情况:bf(F) = +2 和 bf(B) = -1,解决方案:先 rotateLeft(B) 将此情况转变为左左情况,然后转到步骤1
- 右右情况:bf(B) = -2 和 bf(D) = -1,解决方案:rotateLeft(B)
- 右左情况:bf(B) = -2 和 bf(F) = +1,解决方案:先 rotateRight(F) 将此情况转变为右右情况,然后转到步骤3
- 只需像普通BST一样插入v,
- 从插入点向上走AVL树回到根。每走一步,我们更新受影响顶点的高度和平衡因子:
- 如果有的话,停止在不平衡的第一个顶点(+2或-2),
- 使用四个树旋转案例中的一个来重新平衡它,例如 在上面的例子上尝试并通过调用 rotateLeft(29) 解决不平衡问题。
- 如果有的话,停止在不平衡的第一个顶点(+2或-2),
讨论:AVL Tree的 Insert(v) 操作是否还有其他树旋转情况?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
- 只需删除正常BST中的v(三个删除案例中的一个),
- 在AVL树种从删除点向上走回根节点,每一步,我们都会更新受影响的顶点的高度和平衡因子:
- 现在,对于每个不平衡的顶点(+2或-2),我们使用四个树旋转情况中的一个来重新平衡它们(可能多于一个)。
- 现在,对于每个不平衡的顶点(+2或-2),我们使用四个树旋转情况中的一个来重新平衡它们(可能多于一个)。
与AVL树中的 Insert(v) 相比的主要区别在于,我们可能会多次触发四种可能的重新平衡情况中的一种,但不会超过 h = O(log N) 次 :O。在上面的示例中尝试,能看到连锁反应rotateRight(6) 然后rotateRight(16) + rotateLeft(8)。
We have now see how AVL Tree defines the height-balance invariant, maintain it for all vertices during Insert(v) and Remove(v) update operations, and a proof that AVL Tree has h < 2 * log N.
Therefore, all BST operations (both update and query operations except Inorder Traversal) that we have learned so far, if they have time complexity of O(h), they have time complexity of O(log N) if we use AVL Tree version of BST.
This marks the end of this e-Lecture, but please switch to 'Exploration Mode' and try making various calls to Insert(v) and Remove(v) in AVL Tree mode to strengthen your understanding of this data structure.
PS: If you want to study how these seemingly complex AVL Tree (rotation) operations are implemented in a real program, you can download this AVLDemo.cpp | java (must be used together with this BSTDemo.cpp | java).
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
关于这个数据结构的一些更有趣的问题,请在BST/AVL培训模块上进行练习(无需登录)。
然而,对于注册用户,您应该登录并从主页点击培训图标来正式完成这个模块,这样的成就将会被记录在您的用户账户中。
我们还有一些编程问题需要使用这种平衡的BST(如AVL Tree)数据结构:Kattis - compoundwords和Kattis - baconeggsandspam。
尝试使用它们来巩固和提高您对此数据结构的理解。 如果这样可以简化您的实现,则可以使用C ++ STL map / set或Java TreeMap / TreeSet。
尝试使用它们来巩固和提高您对此数据结构的理解。你可以使用 C++ STL map/set,Java TreeMap/TreeSet,或 OCaml Map/Set 来简化您的实现。请注意 Python 没有内置的平衡 BST 的实现。
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
You have reached the last slide. Return to 'Exploration Mode' to start exploring!
Note that if you notice any bug in this visualization or if you want to request for a new visualization feature, do not hesitate to drop an email to the project leader: Dr Steven Halim via his email address: stevenhalim at gmail dot com.
Toggle BST Layout
新建
搜索(v)
插入(v)
移除(v)
前驱/后继(v)
选择
(k)Traverse(root)