Senarai berantai adalah struktur data yang terdiri dari sekumpulan simpul-simpul (vertices/nodes) yang secara keseluruhan merepresentasikan sebuah barisan. Dalam rupa sederhana, tiap simpul yang ada terdiri dari sebuah data dan sebuah referensi (dalam kata lain, rantai) ke simpul berikutnya dalam barisan tersebut. Coba klik Search(77) untuk animasi contoh pencarian sebuah nilai dalam Senarai Berantai Tunggal.

Senarai berantai dan varian-variannya digunakan sebagai struktur data dasar untuk mengimplementasikan ADT Daftar (List), Tumpukan (Stack), Antrean (Antrean), dan Antrean Dua Arah (Deque) (baca artikel Wikipedia tentang ADT jika anda tidak paham dengan terminologi tersebut).

Dalam visualisasi ini, kita akan mendiskusikan senarai berantai tunggal — dengan satu pointer berikutnya — dan dua variannya: Tumpukan (Stack) dan Antrean (Queue), dan juga senarai berantai ganda — dengan pointer berikutnya dan sesudahnya — dan variannya: Antrean Dua Arah (Deque).

Kami memutuskan untuk menggabungkan lima mode-mode yang berhubungan dengan Senarai Berantai (LL, Tumpukan, Antrean, DLL, Deque) didalam sebuah halaman visualisasi saja. Untuk memfasilitasi keberagaman, kami mengacak mode terpilih saat anda mengakses URL langsung ini: https://visualgo.net/en/list.

Tetapi, anda bisa menggunakan shortcut URL dibawah ini untuk mengakses mode tersendiri secara langsung:

1. https://visualgo.net/en/ll,
2. https://visualgo.net/en/stack,
3. https://visualgo.net/en/queue,
4. https://visualgo.net/en/dll,
5. https://visualgo.net/en/deque.

Struktur data Senarai Berantai biasanya diajarkan dalam mata kuliah Ilmu Komputer (Computer Science, CS) karena berbagai alasan-alasan:

1. Struktur data ini sederhana dan linear,
2. Struktur data ini memiliki banyak potensi aplikasi-aplikasi sebagai ADT list misalkan daftar murid, daftar even, daftar perjanjian, dsb (meskipun ada beberapa struktur-struktur data yang lebih tingkat lanjut yang bisa melakukan aplikasi-aplikasi yang sama (dan lebih) dengan lebih baik) atau sebagai ADT tumpukan/antrean/deque,
3. Struktur data memiliki beberapa kasus corner/spesial untuk mengilustrasikan kebutuhan akan implementasi yang baik dari sebuah struktur data,
4. Struktur data ini memiliki berbagai opsi-opsi kustomisasi dan sehingga struktur data Senarai Berantai ini biasanya diajarkan menggunakan cara Object-Oriented Programming (OOP).

Daftar adalah sebuah urutan dari item-item/data dimana urutan posisi penting {a₀, a₁, ..., a_N-2, a_N-1}.
Operasi-operasi ADT Daftar yang umum adalah:

0. get(i) — mungkin operasi yang trivial, kembalikan a_i (indeks berbasis-0),
1. cari(v) — tentukan apabila item/data v ada (dan laporkan posisi/indeksnya)
   atau tidak ada (dan biasanya laporkan sebuah indeks yang tidak ada -1) dalam daftar,
2. masukkan(i, v) — masukkan item/data v secara spesifik pada posisi/indeks i dalam daftar, yang mungkin akan menggeser item-item dari posisi-posisi sebelumnya: [i..N-1] ke satu posisi di kanan mereka untuk membuat sebuah ruang,
3. hapus(i) — hapus item yang secara spesifik berada pada posisi/indeks i dalam daftar, yang mungkin akan menggeser item-item dari posisi-posisi sebelumnya: [i+1..N-1] ke satu posisi di kiri mereka untuk menutup celah,

Diskusi: Bagaimana bila kita mau menghapus item dengan nilai spesifik tertentu v dalam daftar tersebut?

Larik (Padat) adalah sebuah kandidat baik untuk mengimplementasikan ADT Daftar karena itu adalah konstruksi sederhana untuk mengurus sebuah koleksi dari item-item.

Ketika kita membahas larik padat, kita merujuk kepada larik yang tidak mempunyai celah, yaitu jika ada N item-item dalam larik (yang memiliki ukuran M, dimana M ≥ N), maka hanya indeks [0..N-1] yang terisi dan indeks-indeks lain [N..M-1] harus tetap kosong.

Biar nama dari larik padat adalah A dengan indeks [0..N-1] terisi dengan item-item dari daftar.

get(i), kembalikan A[i] saja.
Operasi sederhana ini akan jadi rumit yang tidak perlu jika lariknya tidak padat.

cari(v), kita mengecek setiap indeks i ∈ [0..N-1] satu demi satu untuk melihat apakah A[i] == v.
Ini karena v (jika ada) bisa berada dimanapun di indeks [0..N-1].

masukkan(i, v), kita menggeser item-item ∈ [i..N-1] ke [i+1..N] (dari belakang) dan set A[i] = v.
Ini supaya v dimasukkan dengan benar pada indeks i dan kita menjaga kepadatan.

remove(i), kita menggeser item-item ∈ [i+1..N-1] ke [i..N-2], menimpa nilai A[i] yang lama.
Ini untuk menjaga kepadatan.

get(i) sangat cepat: Hanya satu akses, O(1).
Sebuah modul CS lainnya: 'Organisasi Komputer' mendiskusikan detil-detil tentang performa O(1) dari operasi indeks larik ini.

cari(v)
Pada kasus terbaik, v ditemukan pada posisi pertama, O(1).
Pada kasus terjelek, v tidak ditemukan di daftar dan kita membutuhkan pemindaian dalam O(N) untuk menentukan hal itu.

insert(i, v)
Pada kasus terbaik, pemasukkan pada i = N, tidak ada penggeseran elemen, O(1).
Pada kasus terjelek, pemasukkan pada i = 0, kita harus menggeser semua N element-elemen, O(N).

remove(i)
Pada kasus terbaik, penghapusan pada i = N-1, tidak ada penggesearan elemen, O(1).
Pada kasus terjelek, penghapusan padai = 0, kita harus menggeser semua N element-elemen, O(N).

Ukuran dari larik padat M tidak tak-terbatas, tetapi terbatas. Ini menimbulkan masalah karena ukuran maksimum mungkin tidak diketahui dimuka pada banyak aplikasi-aplikasi.

Jika M terlalu besar, maka ruang-ruang yang tidak terpakai akan terbuang.
Jika M terlalu kecil, maka kita akan kehabisan ruang dengan mudah.

Solusi: Buat M sebagai variabel. Jadi ketika lariknya penuh, kita buat larik yang lebih besar (biasanya dua kali lebih besar) dan pindahkan elemen-elemen dari larik lama ke larik baru. Sehingga, tidak ada lagi batasan dari ukuran kecuali ukuran memori komputer fisik (yang biasanya besar).

C++ STL std::vector, Python list, Java Vector, atau Java ArrayList semua mengimplementasikan larik ukuran-variabel ini.

Tetapi, isu-isu klasik berbasis-array seperti pemborosan ruang dan overhead karena mengkopi/menggeser item-item tetap problematik.

Untuk koleksi-koleksi dengan ukuran-tetap dengan pengetahuan tentang limit maksimum jumlah item-item yang akan pernah dibutuhkan, yaitu ukuran maksimum dari M, larik adalah struktur data yang sudah lumayan bagus untuk implementasi ADT Daftar.

Untuk koleksi-koleksi dengan ukuran-variabel dengan ukuran M yang tidak diketahui dan dimana operasi-operasi dinamis seperti pemasukkan/penghapusan cukup sering digunakan, sebuah larik sederhana sebenarnya adalah pilihan struktur data yang jelek.

Untuk aplikasi-aplikasi seperti itu, ada struktur-struktur data lain yang lebih baik. Mari lanjutkan baca...

Kami sekarang memperkenalkan struktur data Senarai Berantai. Struktur data ini menggunakan pointer untuk membuat item/data menjadi non-contiguous dalam memori (ini adalah perbedaan terbesar dibandingkan dengan sebuah larik sederhana). Item-item terurut dari indeks 0 ke indeks N-1 dengan mengasosiasikan item i dengan tetangganya item i+1 melalui sebuah pointer.

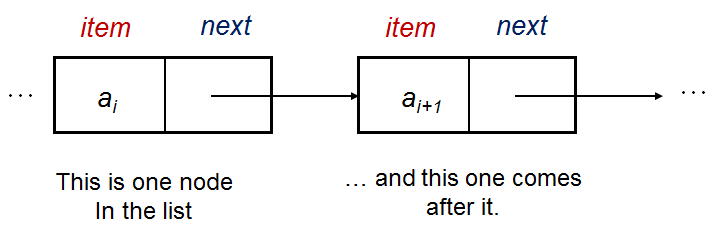
Pada bentuk paling dasar, sebuah simpul (node) tunggal dalam Senarai Berantai memiliki struktur kasar seperti ini:

struct Vertex { // kita bisa memakai C struct atau C++/Python/Java class
  int item; // data ada disini, sebuah bilangan bulat di contoh ini
  Vertex* next; // petunjuk ini menunjuk ke simpul berikut
};

Menggunakan contoh default Senarai Berantai [22 (kepala)->2->77->6->43->76->89 (ekor)]  sebagai ilustrasi, kita punya:
a₀ dengan item = 22 dan next = a₁,
a₁ dengan item = 2 dan next = a₂,
...
a₆ dengan item = 89 dan next = null.

Diskusi: Yang mana yang lebih baik untuk sebuah implementasi C++ dari Senarai Berantai? struct atau class? Bagaimana dengan implementasi Python atau Java?

We also have a few additional data that we remember in this Linked List data structure. We use the default example Linked List [22 (head)->2->77->6->43->76->89 (tail)] for illustration.

1. The head pointer points to a₀ — it is 22, nothing points to the head item,
2. The current number of elements N in the Linked List — N = 7 elements.
3. The tail pointer points to a_N-1 — it is a₆ = 89, nothing is after the tail item.

That's it, we only add three more extra variables in data structure.

Catat bahwa ada beberapa perbedaan-perbedaan kecil yang ditemukan di banyak buku-buku teks Ilmu Kompuer (Computer Science) tentang bagaimana caranya mengimplementasikan sebuah Senarai Berantai (Tunggal) (misalkan menggunakan petunjuk ekor atau tidak, sirkular atau tidak, menggunakan kepala dummy atau tidak) — lihat slide ini.

Versi kami dalam visualisasi ini (dengan petunjuk ekor, tidak sirkular, tanpa kepala dummy) mungkin tidak 100% sama dibandingkan dengan apa yang anda pelajari di kelas anda tetapi ide-ide dasarnya harusnya tetap mirip.

Dalam visualisasi ini, setiap simpul memiliki item bilangan bulat, tetatpi ini bisa dengan mudah diganti menjadi tipe data lainnya seperlunya.

Karena kita hanya menyimpan penunjuk-penunjuk kepala dan ekor, subrutin penjelajahan daftar dibutuhkan untuk mencapai posisi-posisi diluar kepala (indeks 0) dan ekor (indeks N-1).

Karena sub-rutin ini sering sekali dipakai, kita akan mengabstraksikannya sebagai sebuah fungsi. Kode dibawah ditulis dalam bahasa C++.

Vertex* Get(int i) { // kembalikan sebuah simpul
  Vertex* ptr = head; // kita harus mulai dari kepala
  for (int k = 0; k < i; k++) // maju ke depan i kali
    ptr = ptr->next; // penunjuk menunjuk ke indeks lebih tinggi
  return ptr;
}

Sub-rutin ini berjalan dalam O(N) karena i bisa sebesar indeks N-2.
Bandingkan ini dengan larik dimana kita bisa mengakses indeks i dalam waktu O(1).

Karena kita hanya memiliki referensi langsung ke item kepala yang pertama dan item ekor yang terakhir, ditambah lagi semua penunjuk-penunjuk menunjuk ke kanan (posisi/indeks yang lebih tinggi), kita hanya bisa mengakses yang lainnya dengan memulai dari item kepala dan menelusuri penunjuk-penunjuk berikutnya. Pada [22 (kepala)->2->77->6->43->76->89 (ekor)] default, kita punya::

Search(77) — ditemukan pada contoh diatas pada posisi/indeks 2 (indeks berbasis-0).

Search(7) — tidak ditemukan pada contoh diatas, dan ini hanya dapat diketahui setelah semua N item diperiksa, jadi Cari(v) memiliki kompleksitas waktu terjelek sebesar O(N).

There are more cases than array version due to the nature of Linked List.

Most CS students who learn Linked List for the first time usually are not aware of all cases until they figure it out themselves when their Linked List code fail.

In this e-Lecture, we directly elaborate all cases.

For insert(i, v), there are four (legal) possibilities, i.e., item v is added to:

1. The head (before the current first item) of the linked list, i = 0,
2. An empty linked list (which fortunately similar to the previous case),
3. The position beyond the last (the current tail) item of the linked list, i = N,
4. The other positions of the linked list, i = [1..N-1].

Kode (C++) untuk pemasukkan pada kepala mudah dan efisien, dalam O(1):

Vertex* vtx = new Vertex(); // buat simpul baru vtx dari item v
vtx->item = v;
vtx->next = head; // hubungkan simpul baru ini ke simpul kepala (lama)
head = vtx; // simpul baru menjadi kepala yang baru

Coba InsertHead(50), yaitu masukkan(0, 50), pada contoh Senarai Berantai [22 (kepala)->2->77->6->43->76->89 (ekor)] .

Diskusi: Apa yang terjadi jika kita menggunakan implementasi larik untuk pemasukkan pada kepala dari daftar?

Struktur data kosong adalah sebuah kasus sudut/spesial yang umum yang sering menyebabkan crash yang tidak dikehendaki jika tidak diuji dengan baik. Adalah legal untuk memasukkan sebuah item baru ke daftar yang saat ini kosong, yaitu pada indeks i = 0. Untungnya, pseudo-code yang sama untuk pemasukkan pada kepala juga bisa dipakai untuk daftar yang kosong sehingga kita bisa langsung menggunakan kode yang sama seperti di slide ini (dengan satu perubahan minor, kita juga perlu mengeset ekor = kepala).

Coba InsertHead(50), yaitu masukkan(0, 50), tetapi pada Senarai Berantai kosong [].

Dengan sub-rutin penjelajahan Senarai Berantai Get(i), kita sekarang bisa mengimplementasikan pemasukkan di tengah Senarai Berantai sebagai berikut (dalam C++):

Vertex* pre = Get(i-1); // pergi ke simpul (i-1), O(N)
aft = pre.next // aft tidak bisa null, pikirkanlah
Vertex vtx = new Vertex(); // buat simpul baru
vtx->item = v;
vtx->next = aft; // hubungkan ini
pre->next = vtx; // dan ini

Coba Insert(3, 44) pada contoh Senarai Berantai [22 (kepala)->2->77->6->43->76->89 (ekor)] .

Juga coba Insert(6, 55) pada contoh Senarai Berantai yang sama. Ini adalah kasus sudut: Pemasukan pada posisi item ekor, menggeser ekor ke satu posisi ke kanan.

Operasi ini lambat, O(N), karena perlunya menjelajahi daftar (jika i dekat dengan N-1).

Jika kita juga mengingat petunjuk ekor seperti implementasi dalam kuliah maya ini (yang dianjurkan karena itu hanyalah satu tambahan variabel petunjuk), kita bisa melakukan pemasukan setelah item ekor (pada i = N) dengan efisien, dalam O(1):

Vertex* vtx = new Vertex(); // ini juga adalah kode C++
vtx->item = v; // buat simpul baru vtx dari item v
tail->next = vtx; // hubungkan saja, ekor adalah item ke i = (N-1)
tail = vtx; // sekarang mutakhirkan petunjuk ekor

Coba InsertTail(10), yaitu masukkan(7, 10), pada contoh Senarai Berantai [22 (kepala)->2->77->6->43->76->89 (ekor)] . Sebuah miskonsepsi umum adalah untuk mengatakan bahwa ini adalah pemasukkan pada ekor. Pemasukkan pada elemen ekor adalah masukkan(N-1, v). Pemasukan setelah ekor adalah masukkan(N, v).

Diskusi: Apa yang terjadi jika kita menggunakan implementasi larik untuk pemasukkan setelah ekor dari sebuah daftar?

Untuk hapus(i), ada tiga kemungkinan-kemungkinan (legal), yaitu indeks i adalah:

1. Kepala (item yang sekarang pertama) dari senarai berantai, i = 0, ini mempengaruhi penunjuk kepala
2. Ekor dari senarai berantai, i = N-1, ini mempengaruhi penunjuk ekor
3. Posisi-posisi lain dari senarai berantai, i = [1..N-2].

Diskusi: Bandingkan slide ini dengan slide Kasus-Kasus Pemasukkan untuk menyadari perbedaan yang halus. Apakah menghapus sesuatu dari Senarai Berantai yang sudah kosong dapat dikatkan 'legal'?

Kasus ini langsung saja (ditulis dalam C++):

if (head == NULL) return; // hindari crash ketika SLL kosong
Vertex* temp = head; // supaya kita bisa menghapusnya nanti
head = head->next; // pencatatan, mutakhirkan petunjuk kepala
delete temp; // yang adalah kepala yang lama

Cobalah RemoveHead() berulang kali pada contoh Senarai Berantai (yang lebih pendek) [22 (kepala)->2->77->6 (ekor)]. Operasi ini akan terus berjalan dengan benar sampai Senarai Berantai berisi satu item dimana item kepala = ekor. Kami mencegah eksekusi jika Senarai Berantai telah kosong karena itu adalah kasus ilegal.

Diskusi: Apa yang terjadi jika kita menggunakan implementasi larik untuk penghapusan kepala dari sebuah daftar?

Dengan sub-rutin penjelajahan Senarai Berantai Get(i) (yang telah dibahas sebelumnya), kita sekarang dapat mengimplementasikan penghapusan item ditengah-tengah sebuah Senarai Berantai sebagai berikut (dalam bahasa C++):

Vertex* pre = Get(i-1); // pergi ke simpul ke-(i-1), O(N)
Vertex* del = pre->next, aft = del->next;
pre->next = aft; // lewati del
delete del;

Coba Remove(5), elemen pada indeks N-2 (N = 7 pada contoh [22 (kepala)->2->77->6->43->76->89 (ekor)] ).
Ini adalah kasus O(N) terjelek pada contoh diatas.

Catat bahwa Hapus(N-1) adalah penghapusan pada ekor yang membutuhkan pemutakhiran dari petunjuk ekor, lihat kasus setelah ini.

Kita dapat mengimplementasikan penghapusan ekor dari Senarai Berantai sebagai berikut, asumsikan bahwa Senarai Berantai memiliki lebih dari 1 item (dalam bahasa C++):

Vertex* pre = head;
temp = head->next;
while (temp->next != null) // ketika tetangga saya bukan ekor
  pre = pre->next, temp = temp->next;
pre->next = null;
delete temp; // temp = ekor (lama)
tail = pre; // mutakhirkan petunjuk ekor

Coba RemoveTail() berulang kali pada contoh Senarai Berantai (lebih pendek) [22 (kepala)->2->77->6 (ekor)]. Operasi ini akan terus berjalan dengan benar sampai Senarai Berantai berisi satu item dimana item kepala = ekor dan kita berpindah ke kasus penghapusan pada kepala. Kita mencegah eksekusi operasi ini jika Senarai Berantainya sudah kosong karena hal itu adalah kasus ilegal.

Sesungguhnya, jika kita juga menyimpan ukuran dari Senarai Berantai N (bandingkan dengan slide ini), kita dapat menggunakan sub-rutin penjelajahan Senarai Berantai Get(i) untuk mengimplementasikan penghapusan dari ekor dari sebuah Senarai Berantai seperti ini (dalam bahasa C++):

Vertex* pre = Get(N-2); // pergi ke satu indeks dibelakang ekor, O(N)
pre->next = null;
delete tail;
tail = pre; // kita punya akses ke ekor yang lama

Sadari bahwa operasi ini lambat, O(N), hanya karena kita butuh untuk memutakhirkan petunjuk ekor dari item N-1 kebelakang sebesar satu unit ke item N-2 sehingga pemasukkan setelah ekor di masa mendatang tetap benar... Kelemahan ini akan nantinya diatasi dalam varian Senarai Berantai Ganda (Doubly Linked List).

Diskusi: Apa yang terjadi jika kita menggunakan implementasi larik untuk penghapusan dari ekor dari sebuah daftar?

get(i) pelan: O(N).
Dalam Senarai Berantai, kita perlu untuk melakukan akses sekuensial dari elemen kepala.

cari(v)
Pada kasus terbaik, v ditemukan di posisi pertama, O(1).
Pada kasus terjelek, v tidak ditemukan dalam daftar dan kita membutuhkan pemindaian dalam O(N) untuk menentukan hal itu.

masukkan(i, v)
Pada kasus terbaik, pemasukkan pada i = 0 atau pada i = N, penunjuk-penunjuk kepala dan ekor membantu, O(1).
Pada kasus terjelek, pemasukkan pada i = N-1, kita harus mencari item N-2 tepat dibelakang ekor, O(N).

hapus(i)
Pada kasus terbaik, penghapusan pada i = 0, penunjuk kepala membantu, O(1).
Pada kasus terjelek, penghapusan pada i = N-1, karena kita butuh untuk memutakhirkan penunjuk ekor, O(N).

Aplikasi-aplikasi murni dari Senarai Berantai (Tunggal) secara mengejutkan ternyata jarang karena larik padat yang bisa diubah ukurannya (vector) bisa melakukan tugas dengan lebih baik, bandingkan versi Senarai Berantai dengan versi larik padat.

Tetapi, konsep dasar dari Senarai Berantai yang mengijinkan simpul-simpul tidak berdekatan di memori membuatnya menjadi struktur data yang bisa berubah-ukuran yang efisien untuk dua Tipe Data Abstrak berikutnya: Tumpukan dan Antrean.

Tumpukkan adalah sebuah struktur data abstrak di mana operasi utama pada koleksi adalah tambahan terhadap nilai-nilai kedalam koleksi, disebut sebagau push, hanya ke bagian atas tumpukan dan penghapusan nilai yang sudah ada, disebut sebagai pop, hanya dari bagian atas tumpukan.

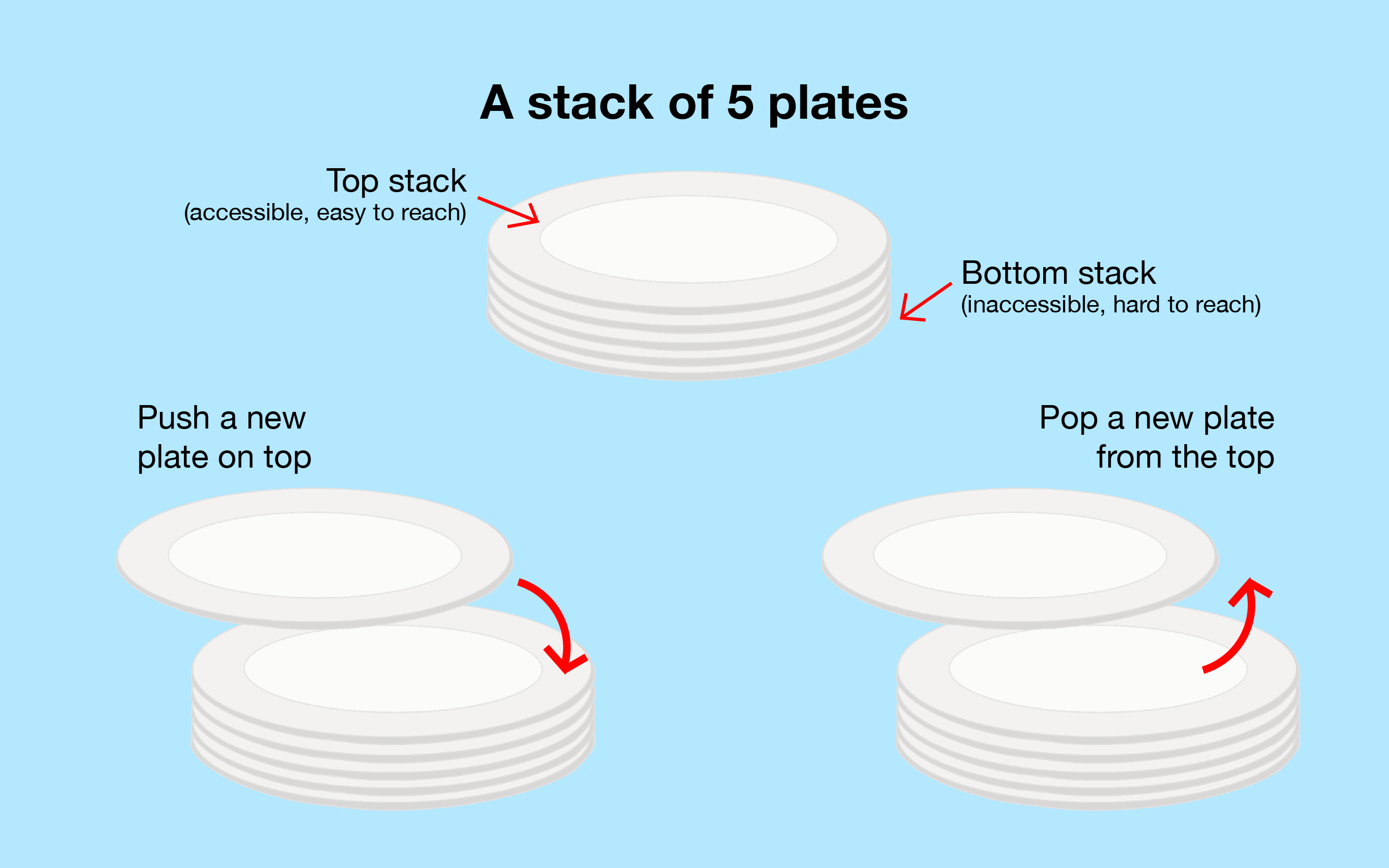
Dalam kebanyakan implementasi-implementasi dan juga dalam visualisasi ini, Tumpukan biasanya adalah Senarai Berantai (Tunggal) dimana kita hanya dapat melihat ke item kepala, memasukkan sebuah item baru hanya ke kepala (pemasukkan di kepala), misalkan coba InsertHead(6), dan pop item yang sudah eksis hanya dari kepala (hapus dari kepala), misalkan coba RemoveHead(). Semua operasi-operasi adalah O(1).

Dalam visualisasi ini, kita me mengorientasikan Senarai Berantai (Tunggul) dari atas kebawah, dengan item kepala/ekor masing-masing pada posisi atas/bawah. Pada contoh, kita punya [2 (atas/kepala)->7->5->3->1->9 (bawah/ekor)].

Diskusi: Bisakah kita menggunakan vector, larik yang bisa berubah ukuran, untuk mengimplementasikan ADT Tumpukan dengan efisien?

Tumpukan memiliki beberapa aplikasi-aplikasi buku teks yang popular, yaitu:

1. Pencocokan Kurung,
2. Perhitungan Postfix,
3. Beberapa aplikasi-aplikasi lain yang menarik yang tidak ditunjukkan karena alasan pedagogis.

Ekspresi matematika bisa cukup berbelit-belit, seperti {[x+2]^(2+5)-2}*(y+5).

Masalah Pencocokan Tanda-Kurung adalah sebuah masalah pengecekan apabila semua tanda-tanda kurung yang diberikan dalam masukan dapat dicocokkan dengan benar, yaitu ( dengan ), [ dengan ] dan { dengan }, dan sebagainya.

Pencocokan Tanda-Kurung juga berguna untuk mengecek legalitas dari sebuah kode sumber.

Diskusi: Kita bisa pakai sifat LIFO dari Tumpukan untuk menyelesaikan masalah ini.
Pertanyaannya: Bagaimana?

Ekspresi Postfix adalah ekspresi matematika dalam format: operand1 operand2 operator yang adalah berbeda dengan apa yang paling nyaman untuk manusia, yaitu ekspresi Infix: operand1 operator operand2.

Contohnya, ekspresi 2 3 + 4 * adalah versi Postfix dari (2+3)*4.

Dalam ekspresi Postfix, kita tidak memerlukan tanda-tanda kurung.

Diskusi: Kita bisa pakai Tumpukan untuk menyelesaikan masalah ini secara efisien.
Pertanyaannya: Bagaimana?

Antrean adalah sebuah struktur data abstrak di mana item-item dalam koleksi dipertahankan urutannya dan operasi-operasi utama yang dapat dilakukan pada koleksi adalah menambahkan item-item ke posisi belakang (enqueue) dan menghapus item-item dari posisi depan (dequeue).

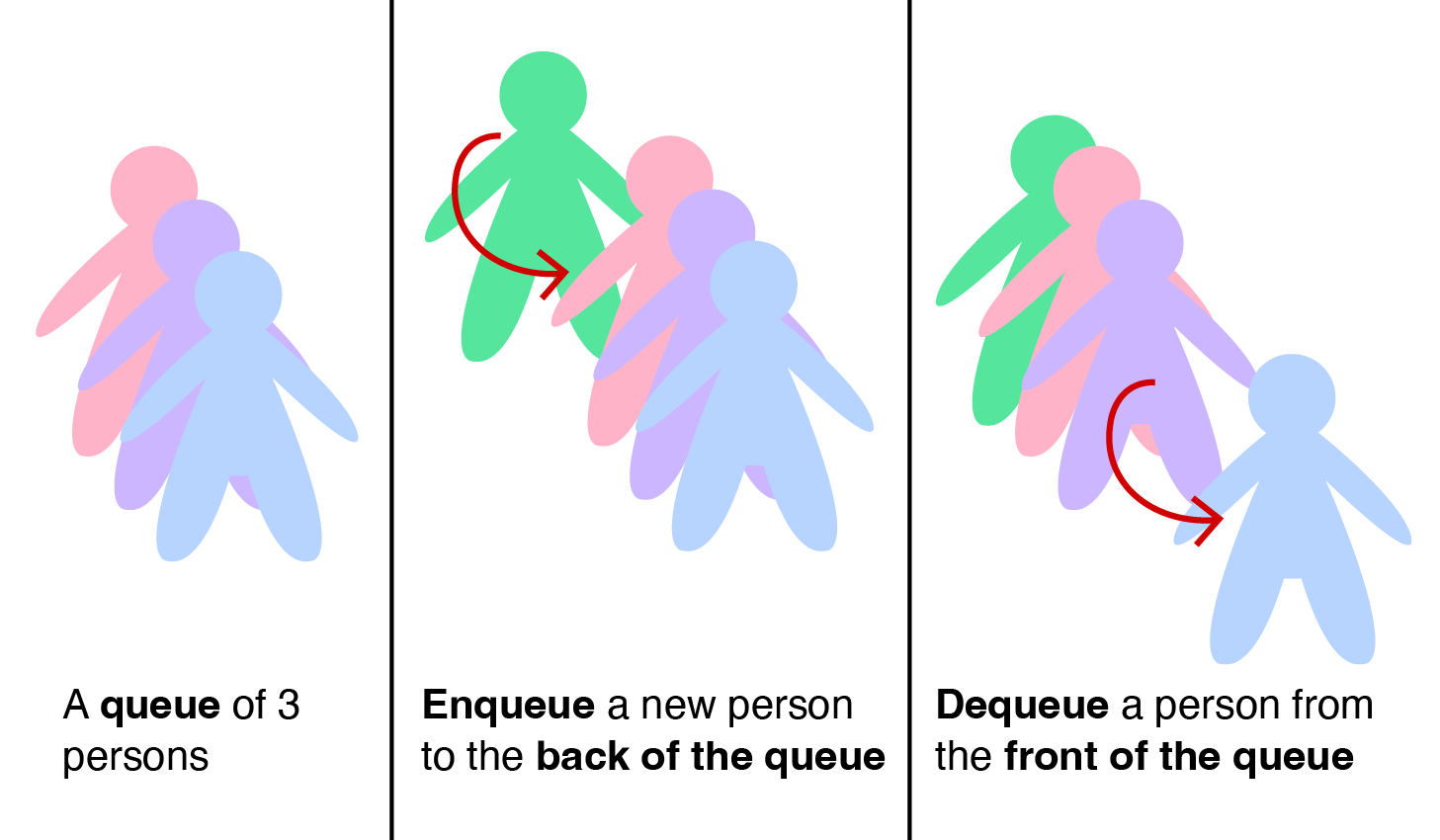
Jika kita secara sederhana menggunakan implementasi larik padat untuk ADT Antrean ini dengan a₀ sebagai depan dari antrean dan a_N-1 sebagai belakang dari antrean, kita akan menjumpai isu performa yang mayor dengan operasi dequeue.

Ini karena pemasukkan pada posisi belakang dari larik padat itu cepat, O(1), tetapi penghapusan pada depan dari larik padat adalah lambat karena kita butuh untuk menggeser item-item, silahkan ulas slide ini.

Sebuah implementasi larik yang lain adalah menghindari penggeseran item-item selama operasi dequeue dengan menggunakan dua indeks: depan (indeks dari item paling-depan dari antrean, yang akan dinaikkan setelah sebuah operasi dequeue) dan belakang (indeks dari item paling-belakang dari antrean, juga dinaikkan setelah sebuah operasi enqueue).

Misalkan kita menggunakan sebuah larik dengan ukuran M = 8 item-item dan isi dari antrean kita adalah sebagai berikut: [2,4,1,7,-,-,-,-] dengan depan = 0 dan belakang = 3.

Jika kita memanggil dequeue, kita mendapatkan [-,4,1,7,-,-,-,-], depan = 0+1 = 1, dan belakang = 3.

Jika kita lalu memanggil enqueue(5), kita mendapatkan [-,4,1,7,5,-,-,-], depan = 1, dan belakang = 3+1 = 4.

Tetapi, banyak operasi dequeue dan enqueue berikutnya, kita mungkin mendapat [-,-,-,-,-,6,2,3], depan = 5, dan belakang = 7. Pada titik ini, kita tidak bisa meng-enqueue apapun lagi meskipun kita masih mempunyai banyak ruang-ruang kosong di depan larik.

Jika kita mengijinkan indeks-indeks depan dan belakang untuk "melipat balik" ke indeks 0 ketika mereka telah mencapai indeks M-1, kita secara efektif membuat larik tersebut "sirkular" dan kita bisa menggunakan ruang-ruang kosong yang ada.

Contohnya, jika kita memanggil enqueue(8) berikutnya, kita mendapatkan [8 , -,-,-,-,6,2,3], depan = 5, dan belakang = (7+1)%8 = 0.

Ini tidak menyelesaikan masalah utama dari implementasi larik: Item-item dari sebuah larik disimpan secara bersebelahan (contiguous) dalam memori komputer.

Beberapa operasi-operasi enqueue berikutnya, kita mungkin mendapat [8,10,11,12,13 , 6,2,3], depan = 5, dan belakang = 4. Pada titik ini, kita tidak dapat meng-enqueue apapun lagi.

Kita dapat memperbesar larik, yaitu membuat M = 2*8 = 16, tetapi itu berarti kita harus meng-kopi item-item dari indeks depan ke belakang dalam proses O(N) yang lambat untuk mendapatkan [6,2,3,8,10,11,12,13,-,-,-,-,-,-,-,-,], depan = 0, dan belakang = 7.

Catatan: Jika anda mengerti tentang analisa amortisasi, harga O(N) yang berat ini ketika larik melingkar penuh sebenarnya bisa disebar sehingga tiap masukan tetap O(1) secara amortisasi.

Dalam sebuah Antrean, kita hanya memerlukan dua ujung ekstrim dari Daftar, satu untuk pemasukkan (enqueue) saja dan satu untuk penghapusan (dequeue) saja.

Jika kita mengulas slide ini, kita akan melihat bahwa pemasukkan setelah ekor dan penghapusan dari kepala dalam sebuah Senarai Berantai Tunggal adalah cepat, yaitu dalam O(1). Jadi, kita atur kepala/ekor dari sebuah Senarai Berantai Tunggal masing-masing sebagai depan/belakang dari antrean. Lalu, karena item-item dalam sebuah Senarai Berantai tidak disimpan secara berdekatan dalam memori komputer, Senarai Berantai kita bisa membesar dan mengecil seperlunya.

Dalam visualisasi kami, Antrean pada dasarnya adalah Senarai Berantai Tunggal yang terproteksi dimana kita hanya bisa melihat item kepala, memasukkan item baru ke satu posisi setelah ekor yang sekarang, misal coba Enqueue(random-integer), dan dequeue item yang sudah eksis dari kepala, misal coba RemoveHead() (yang secara esensi adalah operasi dequeue). Semua operasi-operasi berjalan dalam O(1).

ADT Antrean biasanya digunakan untuk mensimulasikan antrean-antrean nyata.

Satu aplikasi sangat penting dari ADT Antrean adalah didalam algoritma penjelajahan graf Breadth-First Search.

Masalah utama dari penghapusan elemen ekor dari sebuah Senarai Berantai Tunggal, meskipun kita memiliki akses langsung ke item ekor lewat petunjuk ekor, adalah bahwa kita harus lalu memutakhirkan petunjuk ekor ini agar menunjuk ke item yang berada satu posisi dibelakang ekor setelah penghapusan tersebut.

Dengan kemampuan Senarai Berantai Ganda (Doubly Linked List) untuk berjalan mundur, kita dapat menemukan item yang berada dibelakang ekor lewat tail->prev... Sehingga, kita dapat mengimplementasikan penghapusan dari ekor seperti ini (dalam C++):

Vertex* temp = tail; // ingat item ekor
tail = tail->prev; // langkah kunci untuk mendapat performa O(1) :O
tail->next = null; // hapus referensi kosong ini
delete temp; // hapus ekor lama

Sekarang operasi ini adalah O(1). Coba RemoveTail() pada DLL contoh [22 (kepala)<->2<->77<->6<->43<->76<->89 (ekor)].

Karena kita memiliki satu penunjuk lagi prev untuk setiap simpul, nilai-nilai mereka perlu dimutakhirkan juga pada setiap pemasukkan dan penghapusan. Cobalah semua operasi-operasi berikut pada DLL contoh [22 (kepala)<->2<->77<->6<->43<->76<->89 (ekor)].

Coba InsertHead(50) — langkah tambahan: penunjuk prev 22 menunjuk ke kepala baru 50.

Coba InsertTail(10) — langkah tambahan: penunjuk prev 10 menunjuk ke ekor lama 89.

Coba Insert(3, 44) — langkah tambahan: penunjuk prev 6/44 masing-masing menunjuk ke 44/77.

Coba RemoveHead() — set penunjuk prev kepala baru 2 ke null.

Coba Remove(5) — set penunjuk prev 89 ke 43.

Deque dipakai dalam beberapa aplikasi-aplikasi advanced, seperti mencari jarak terpendek dalam graf berbobot 0/1 menggunakan BFS yang dimodifikasi, pada beberapa teknik sliding window, dan sebagainya.

Kita telah mencapai akhir dari Kuliah Maya ini.

Tapi tetap lanjut membaca untuk melihat beberapa tantangan-tantangan ekstra.

Hal-hal berikut adalah insight yang lebih tingkat lanjut mengenai Senarai Berantai:

1. Apa yang terjadi jika kita tidak menyimpan pointer ekor juga?
2. Bagaimana bila kita menggunakan kepala dummy?
3. Bagaimana bila item ekor terakhir menunjuk kembali ke item kepala?

C++ STL:
forward_list (sebuah Senarai Berantai Tunggal)
stack
queue
list (sebuah Senarai Berantai Ganda)
deque (sebenarnya tidak menggunakan Senarai Berantai Ganda tetapi teknik lain, lihat cppreference)

LinkedList (sudah Senarai Berantai Ganda)
Stack
Queue (sebenarnya interface, biasanya diimplementasikan dengan LinkedList class)
Deque (sebenarnya interface, biasanya diimplementasikan dengan LinkedList class)

Python:
list untuk Senarai Berantai/Tumpukan/Antrean
deque

OCaml:
List
Stack
Queue
Tidak ada dukungan built-in untuk Deque

Untuk beberapa pertanyaan-pertanyaan yang menarik lainnya tentang struktur data ini, silahkan latihan pada modul latihan Senarai Berantai.

Kami juga memiliki beberapa masalah-masalah pemrograman yang membutuhkan penggunaan dari struktur data Senarai Berantai, Tumpukan, Antrean, atau Deque:
UVa 11988 - Broken Keyboard (a.k.a. Beiju Text), Kattis - backspace, dan Kattis - integerlists.

Cobalah mereka untuk memantapkan dan meningkatkan pengertian anda tentang struktur data ini. Anda diijinkan untuk menggunakan C++ STL, perpustakan standar Python, atau Java API jika itu mempermudah implementasi anda.