


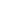




假设你有一个函数 f: S → S 和任何初始值 x0 ∈ S
(在这个可视化中,我们限制为 f(x) = (A*x^2 + B*x + C) % M 和 x0 % M,因此函数 f 的定义域和值域 ∈ [0..M-1])。
迭代函数值的序列:
{x0, x1 = f(x0), x2 = f(x1), ..., xi = f(xi-1), ...}
必须最终使用两次相同的值(循环),即 a ≠ b 使得 xa = xb。
之后,序列必须通过重复从 xa 到 xb-1 的值的循环来继续。
设 mu (μ) 是最小的索引,设 lambda (λ)(循环长度)是最小的正整数,使得 xμ = xμ+λ。
寻找循环问题:给定 f 和 x0,找到这样的 μ 和 λ。
Remarks: By default, we show e-Lecture Mode for first time (or non logged-in) visitor.
If you are an NUS student and a repeat visitor, please login.
您可以在此处定义自定义函数 f(x) = (A*x2 + B*x + C) % M。
- 随机:函数将为 f(x) = (x2 - 1) % M,只有 M 和 x0 是随机生成的。
- 自定义:您可以指定 f(x) 的系数 A、B、C(范围从 -999 到 999),模数值 M(范围从 10 到 1000)和初始值 x0(范围从 0 到 M-1)。
您还可以设置自定义 x0,必须 ∈ [0..M-1]。
Pro-tip 1: Since you are not logged-in, you may be a first time visitor (or not an NUS student) who are not aware of the following keyboard shortcuts to navigate this e-Lecture mode: [PageDown]/[PageUp] to go to the next/previous slide, respectively, (and if the drop-down box is highlighted, you can also use [→ or ↓/← or ↑] to do the same),and [Esc] to toggle between this e-Lecture mode and exploration mode.
Floyd's Tortoise-Hare Cycle-Finding is one algorithm that can solve this problem efficiently in both time and space complexities.
It just requires O(μ+λ) time and O(1) space to do the job.
Pro-tip 2: We designed this visualization and this e-Lecture mode to look good on 1366x768 resolution or larger (typical modern laptop resolution in 2021). We recommend using Google Chrome to access VisuAlgo. Go to full screen mode (F11) to enjoy this setup. However, you can use zoom-in (Ctrl +) or zoom-out (Ctrl -) to calibrate this.
This is the visualization of Floyd's Tortoise-Hare Cycle-Finding algorithm.
The shape of rho (ρ) of the sequence of iterated function values defined by f(x) and x0 nicely visualizes μ and λ.
VisuAlgo uses green vertices to represent the tortoise (t) and orange vertices to represent the hare (h).
Pro-tip 3: Other than using the typical media UI at the bottom of the page, you can also control the animation playback using keyboard shortcuts (in Exploration Mode): Spacebar to play/pause/replay the animation, ←/→ to step the animation backwards/forwards, respectively, and -/+ to decrease/increase the animation speed, respectively.
我们从 x0 开始。
当 乌龟的指针 != 兔子的指针 时,我们通过调用 f(乌龟)/f(f(兔子)) 将 乌龟/兔子 向前推进一步/两步到他们的下一个值。
我们将 hare 重置回 x0,并保持 tortoise 在其当前位置。
然后,我们将两个指针迭代地向前移动一步,因为这样可以保持 tortoise 和 hare 的间隔为 kλ。
两个指针第一次相等时,就告诉我们 μ 的值。
再次,我们让乌龟保持在其当前位置,并将兔子设置在它旁边。
然后,我们通过一步一步地将兔子移动到下一个值。
两个指针第一次相等告诉我们λ的值。
我们将扩展此讲座的幻灯片,以便稍后加入更多有关此算法的信息
You are allowed to use/modify our implementation code for Floyd Cycle-Finding Algorithm:
UVa00350.cpp
UVa00350.java
UVa00350.py
UVa00350.ml
You have reached the last slide. Return to 'Exploration Mode' to start exploring!
Note that if you notice any bug in this visualization or if you want to request for a new visualization feature, do not hesitate to drop an email to the project leader: Dr Steven Halim via his email address: stevenhalim at gmail dot com.
随机
Custom(a, b, c, m, z0)