


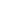




The Union-Find Disjoint Sets (UFDS) data structure is used to model a collection of disjoint sets, which is able to efficiently (i.e., in nearly constant time) determine which set an item belongs to, test if two items belong to the same set, and union two disjoint sets into one when needed. It can be used to find connected components in an undirected graph, and can hence be used as part of Kruskal's algorithm for the Minimum Spanning Tree (MST) problem.
Note that this data structure has another alternative name: Disjoint Sets Union (DSU).
Remarks: By default, we show e-Lecture Mode for first time (or non logged-in) visitor.
If you are an NUS student and a repeat visitor, please login.
View the visualization of a sample Union-Find Disjoint Sets here!
Each tree represents a disjoint set (thus a collection of disjoint sets form a forest of trees) and the root of the tree is the representative item of this disjoint set.
Now stop and look at the currently visualized trees. How many items (N) are there overall? How many disjoint sets are there? What are the members of each disjoint set? What is the representative item of each disjoint set?
Pro-tip 1: Since you are not logged-in, you may be a first time visitor (or not an NUS student) who are not aware of the following keyboard shortcuts to navigate this e-Lecture mode: [PageDown]/[PageUp] to go to the next/previous slide, respectively, (and if the drop-down box is highlighted, you can also use [→ or ↓/← or ↑] to do the same),and [Esc] to toggle between this e-Lecture mode and exploration mode.
As we fixed the default example for this e-Lecture, your answers should be: N=13 and there are 4 disjoint sets: {0,1,2,3,4,10}, {5,7,8,11}, {6,9}, {12} with the underlined members be the representative items (of their own disjoint set).
Pro-tip 2: We designed this visualization and this e-Lecture mode to look good on 1366x768 resolution or larger (typical modern laptop resolution in 2021). We recommend using Google Chrome to access VisuAlgo. Go to full screen mode (F11) to enjoy this setup. However, you can use zoom-in (Ctrl +) or zoom-out (Ctrl -) to calibrate this.
We can simply record this forest of trees with an array p of size N items where p[i] records the parent of item i and if p[i] = i, then i is the root of this tree and also the representative item of the set that contains item i.
Once again, look at the visualization above and determine the values inside this array p.
Discuss: If i is the root of the tree that contains it, can we set p[i] = -1 instead of p[i] = i? What are the implications?
Pro-tip 3: Other than using the typical media UI at the bottom of the page, you can also control the animation playback using keyboard shortcuts (in Exploration Mode): Spacebar to play/pause/replay the animation, ←/→ to step the animation backwards/forwards, respectively, and -/+ to decrease/increase the animation speed, respectively.
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
On the same fixed example, your answers should be p = [1, 3, 3, 3, 3, 5, 6, 5, 5, 6, 4, 8,12] of size N = 13 ranging from p[0] to p[12].
You can check that p[3] = 3, p[5] = 5, p[6] = 6, and p[12] = 12, which are consistent with the fact that {3,5,6,12} are the representative items (of their own disjoint set).
We also record one more information in array rank also of size N. The value of rank[i] is the upperbound of the height of subtree rooted at vertex i that will be used as guiding heuristic for UnionSet(i, j) operation. You will notice that after 'path-compression' heuristic (to be described later) compresses some path, the rank values no longer reflect the true height of that subtree.
As there are many items with rank 0, we set the visualization as follows to minimize clutter: Only when the rank of a vertex i is greater than 0, then VisuAlgo will show the value of rank[i] (abbreviated as a single character r) as a red text below vertex i.
On the same fixed example, verify that {1,4,6,8} have rank 1 and {3,5} have rank 2, with the rest having rank 0 (not shown).
At this point of time, all rank values are correct, i.e., they really describe the height of the subtree rooted at that vertex. We will soon see that they will not be always correct in the next few slides.
There are five available UFDS operations in this visualization page:
Examples, Initialize(N), FindSet(i), IsSameSet(i, j), and UnionSet(i, j).
The first operation (Examples) is trivial: List of example UFDS structures with various special characteristics for your starting point. This e-Lecture mode always use the 'Four disjoint sets' example as the starting point.
Also notice that none of the example contains a 'very tall' tree. You will soon understand the reason after we describe the two heuristics used.
Initialize(N, M): Create N items and form M disjoint sets with these N items. We randomly pick two disjoint sets and merge them until we have M random disjoint sets. Due to the union-by-rank heuristics used and the randomness, it is very unlikely that this initialization process creates a tall tree.
The default form is Initialize(N, N), i.e., M = N, all with p[i] = i and rank[i] = 0 (all these rank values are initially not shown). The time complexity of this operation is clearly O(N).
Due to the limitation of screen size, we set 1 ≤ N ≤ 32. Obviously M ≤ N.
FindSet(i): From vertex i, recursively go up the tree. That is, from vertex i, we go to vertex p[i]) until we find the root of this tree, which is the representative item with p[i] = i of this disjoint set.
In this FindSet(i) operation, we employ path-compression heuristic after each call of FindSet(i) as now every single vertex along the path from vertex i to the root know that the root is their representative item and can point to it directly in O(1).
If we execute FindSet(12), we will immediately get vertex 12.
If we execute FindSet(9) we will get vertex 6 after 1 step and no other change.
Now try executing . If this is your first call on this default UFDS example, it will return vertex 3 after 2 steps and then modify the underlying UFDS structure due to path-compression in action (that is, vertex 0 points to vertex 3 directly). Notice that rank value of rank[1] = 1 is now wrong as vertex 1 becomes a new leaf. However, we will not bother to update its value.
Notice that the next time you execute again, it will be (much) faster as the path has been compressed. For now, we assume that FindSet(i) runs in O(1).
IsSameSet(i, j): Simply check if FindSet(i) == FindSet(j) or not. This function is used extensively in Kruskal's MST algorithm. As it only calls FindSet operation twice, we will assume it also runs in O(1).
Note that FindSet function is called inside IsSameSet function, so path-compression heuristic is also indirectly used.
If we call IsSameSet(3, 5), we should get false as vertex 3 and vertex 5 are representative items of their respective disjoint sets and they are different.
Now try on the same default example to see indirect path-compression on vertex 0 and vertex 11. We should get false as the two representative items: vertex 3 and vertex 5, are different. Notice that the rank values at vertex {1, 5, 8} are now wrong. But we will not fix them.
UnionSet(i, j): If item i and j come from two disjoint sets initially, we link the representative item of the shorter tree/disjoint set to the representative item of the taller tree/disjoint set (otherwise, we do nothing). This is also done in O(1).
This is union-by-rank heuristic in action and will cause the resulting tree to be relatively short. Only if the two trees are equally tall before union (by comparing their rank values heuristically — note that we are not comparing their actual — the current — heights), then the rank of the resulting tree will increase by one unit.
Also note that FindSet function is called inside UnionSet function, so path-compression heuristic is also indirectly used. Each time path-compression heuristic compresses a path, at least one rank values will be incorrect. We do not bother fixing these rank values as they are only used as guiding heuristic for this UnionSet function.
On the same default example, try . As the tree that represents disjoint set {6, 9} is currently taller (according to the value of rank[6] = 1), then the shorter tree that represents disjoint set {12} will be slotted under vertex 6, without increasing the height of the combined tree at all.
On the same default example, try . Notice that the ranks of vertex 3 and vertex 5 are the same rank[3] = rank[5] = 2. Thus, we can either put vertex 3 under vertex 5 (our implementation) or vertex 5 under vertex 3 (both will increase the resulting height of the combined tree by 1). Notice the indirect path-compression heuristic in action.
Quiz: Starting with N=8 disjoint sets, how tall (heuristically) can the resulting final tree if we call 7 UnionSet(i, j) operations strategically?
Quiz: Starting with N=8 disjoint sets, how short (heuristically) can the resulting final tree if we call 7 UnionSet(i, j) operations strategically?
Discussion: Why?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
So far, we say that FindSet(i), IsSameSet(i, j), and UnionSet(i, j) runs in O(1). Actually they run in O(α(N)) if the UFDS is implemented with both path-compression and union-by-rank heuristics. The analysis is quite involved and is skipped in this visualization.
This α(N) is called the inverse Ackermann function that grows extremely slowly. For practical usage of this UFDS data structure (assuming N ≤ 1M), we have α(1M) ≈ 1.
You have reached the end of the basic stuffs of this UFDS data structure and we encourage you to go to Exploration Mode and explore this simple but interesting data structure using your own examples.
However, we still have a few more interesting UFDS challenges for you.
Please look at the following C++/Python/Java/OCaml implementations of this Union-Find Disjoint Sets data structure in Object-Oriented Programming (OOP) fashion: unionfind_ds.cpp | py | java | ml
You are free to customize this implementation to suit your needs as some harder problem requires customization of this basic implementation.
I do wish that one day C++/Python/Java/OCaml/other programming languages will include this interesting data structure in their base libraries.
For a few more interesting questions about this data structure, please practice on Union-Find Disjoint Sets training module.
Even after clearing the Online Quiz of this UFDS module, do you think that you have really mastered this data structure?
Let us challenge you by asking you to solve two programming problems that somewhat requires the usage of this Union-Find Disjoint Sets data structure: UVa 01329 - Corporative Network and Kattis - control.
Beware that both problems are actual International Collegiate Programming Contest (ICPC) problems, i.e., they are "not trivial".
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
Notice that there is no 'undo' operation for Union-Find Disjoint Sets (UFDS) data structure. Once two initially disjoint sets were union-ed, it is not easy to split them back into the original two disjoint sets, especially when path compressions have flattened the combined tree.
Discussion: So what to do if we need this 'de-Union' or 'split' or 'cut' operation?
The content of this interesting slide (the answer of the usually intriguing discussion point from the earlier slide) is hidden and only available for legitimate CS lecturer worldwide. This mechanism is used in the various flipped classrooms in NUS.
If you are really a CS lecturer (or an IT teacher) (outside of NUS) and are interested to know the answers, please drop an email to stevenhalim at gmail dot com (show your University staff profile/relevant proof to Steven) for Steven to manually activate this CS lecturer-only feature for you.
FAQ: This feature will NOT be given to anyone else who is not a CS lecturer.
You have reached the last slide. Return to 'Exploration Mode' to start exploring!
Note that if you notice any bug in this visualization or if you want to request for a new visualization feature, do not hesitate to drop an email to the project leader: Dr Steven Halim via his email address: stevenhalim at gmail dot com.
Examples
Initialize
FindSet
IsSameSet
UnionSet