Sebuah reduksi adalah sebuah cara untuk merubah/transform satu masalah menjadi masalah lain.

Misalkan anda mempunyai masalah A yang anda tidak tahu bagaimana cara menyelesaikannya. Namun, anda tau sebuah algoritma yang menyelesaikan masalah B. Jika anda dapat merubah sebuah instance α dari masalah A menjadi sebuah instance β dari masalah B, anda bisa menggunakan algoritma untuk B untuk menyelesaikan instance β yang sudah diubah, dan mendapatkan solusi α dari solusi β, dengan cara "membalikkan transformasi". Maka, kita bisa menyatakan bahwa A direduksi menjadi B.

Dengan reduksi, kita mempunyai alat lain untuk menyelesaikan masalah.

Diberikan dua masalah desisi A dan B, sebuah reduksi waktu-polinomial dari A ke B,
dinyatakan A ≤_p B, merupakan sebuah transformasi dari is a transformation from instance α dari A to instance β dari B sehingga:

1. α adalah YES-instance untuk A jika dan hanya jika β adalah YES-instance untuk B.
   (Sebuah YES-instance adalah instance dari sebuah masalah desisi yang jawabannya adalah YES/True).
2. Transformasinya memperlukan waktu polinomial terhadap ukuran dari α.

Dengan suatu reduksi waktu-polinomial, kita bisa klaim:
Jika B "mudah dikerjakan", maka A juga.
Jika A "sulit", maka B juga.

Namun, B "sulit" bukan berarti A "sulit".
Dan A "mudah" bukan berarti B "mudah".

Dalam halaman visualisasi (statis, tidak ada animasi) ini, kita ingin menunjukkan jaringan reduksi (yang terkenal) dari masalah desisi NP-complete berbeda ke lainnya. Secara teori, karena semua masalah tersebut adalah NP-complete, mereka semua bisa direduksikan menjadi satu lainnya, tetapi transformasi tersebut bisa menjadi sangat rumit untuk beberapa maslaah.

Jaringan reduksi yang ditunjukkan di halaman ini merupakan gabungan dari "Introductions to Algorithms (CLRS, 4th edition)", 21 masalah NP-complete Karp , "Computers and Intractability (Garey and Johnson, 79), dll.

Sebuah simpul berisi nama singkat dari masalah keputusan NP-complete. Arahkan kursor ke atasnya untuk melihat nama lengkapnya. Anda juga dapat menekan simpul tersebut untuk membuka slide terkait yang secara formal menjelaskan masalah tersebut.

Sebuah tepi terarah antara simpul membuka slide yang berisi bukti reduksi dari satu masalah ke masalah lainnya, sesuai dengan arah panah, seperti yang ditemukan dalam banyak sumber kompleksitas komputasi (buku/Internet/dll). Bukti reduksi umumnya berbentuk jika dan hanya jika (iff). Panah hijau menunjukkan bahwa kami telah mendigitalkan bukti reduksi tersebut. Panah hitam menunjukkan bahwa kami belum melakukannya. Kami berharap dapat menambahkan konten sebanyak mungkin ke halaman ini secara bertahap dari waktu ke waktu.

Masalah CIRCUIT-SATISFIABILITY (C-SAT) merupakan sebuah masalah desisi tentang menentukan jika sebuah sirkuit Boolean - pada dasarnya sebuah DAG - (menggunakan gate AND ∧, OR ∨, NOT ¬) mempunyai sebuah penugasan dari n masukan biner yang membuat keluaran menjadi True (1). Dalam kata lain, masalah ini menanyakan apakah n masukan biner bisa diset menjadi True (1) atau False (0) secara konsisten sehingga sirkuit tersebut mengeluarkan True (1). Jikalau demikian, sirkuit tersebut memenuhi. Jika tidak, sirkuit tersebut tidak memenuhi.

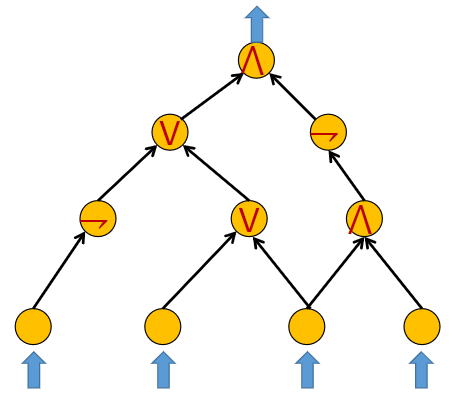YES-instance (Contoh Sertifikat: False, True, True, False)

Hal Penting: L ≤p C-SAT untuk sembarang bahasa L ∈ NP.

Definisi: Literal adalah sebuah variabel Boolean atau negasinya, yakni x_i, x̄_i.
Klausa: Sebuah disjungsi (OR ∨) dari beberapa literal, yakni C_j = x₁ ∨ x̄₂ ∨ x₃.

Masalah CONJUNCTIVE-NORMAL-FORM-SATISFIABILITY (CNF-SAT), atau kadang hanya disebut sebagai SATISFIABILITY (SAT), adalah masalah desisi tentang menentukan jika sebuah formula Φ yaitu konjungsi (AND ∧) dari klausa, yakni, Φ = C₁ ∧ C₂ ∧ C₃ ∧ C₄, mempunyai sebuah penugasan literal yang memenuhi.

Masalah 3-CNF-SAT(isfiability), biasanya hanya disebut dengan 3-SAT, merupakan masalah CNF-SAT di mana tiap klausa mempunyai tepat 3 literal dengan variabel berbeda.

Contohnya: Φ = (x̄₁ ∨ x₂ ∨ x₃) ∧ (x₁ ∨ x̄₂ ∨ x₃) ∧ (x̄₁ ∨ x₂ ∨ x₄) adalah sebuah YES-instance.
(Contoh sertifikat: x₁ = x₂ = x₄ = True, x₃ = False).

Sebuah clique adalah himpunan simpul C dari graf G = (V, E) sehingga ∃ sebuah tepi antara setiap pasangan simpul yang berbeda dalam himpunan tersebut (u, v ∈ C, ∃ (u, v)). Himpunan C adalah subgraf lengkap dari G. Maka, ukuran clique adalah jumlah simpul dalam himpunan C.

Masalah keputusan CLIQUE menanyakan untuk sebuah graf G = (V, E): Apakah ada subgraf lengkap dalam G dengan ukuran setidaknya k?

Diberikan graf G = (V, E), sebuah subset C ⊆ V dikatakan sebagai cover simpul jika untuk setiap sisi (u, v) ∈ E, antara u ∈ C atau v ∈ C.

Diberikan graf G = (V, E), masalah VERTEX-COVER (VC) menanyakan: Apakah ada cover simpul dengan ukuran ≤ k?

Perlu dicatat bahwa kami telah membangun halaman visualisasi mvc khusus yang membahas masalah ini dan berbagai strategi untuk mengatasi masalah ini secara lebih rinci,

Diberikan sebuah graf tak berarah tak berbobot G = (V, E), masalah HAMILTONIAN-CYCLE (HC, terkadang disingkat menjadi HAM-CYCLE) menanyakan:
Apakah terdapat sebuah siklus (sederhana) yang melewati semua simpul tepat sekali?

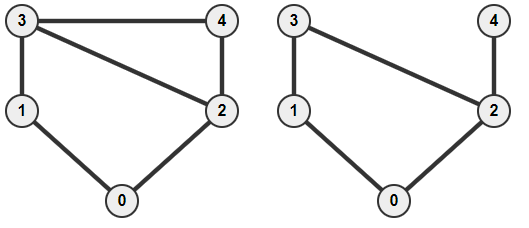
Kiri/YES-instance (Contoh sertifikat: 0-1-3-4-2-0) ------- ------- ------- Kanan/NO-instance

Diberikan sebuah graf komplet tak berarah dengan sisi berbobot tak negatif dan b ∈ R+,
masalah TRAVELING-SALESPERSON-PROBLEM (TSP) menanyakan:
Apakah terdapat tour dengan biaya tidak lebih dari b?

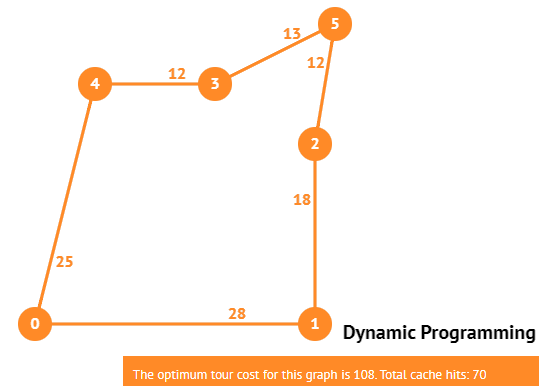
YES-instance untuk b = 108 tapi NO-instance untuk b = 107 karena OPT = 108

Catat bahwa kami telah membuat sebuah laman visualisasi spesial untuk tsp yang membahas masalah ini dan beberapa strategi untuk menyelesaikan masalah ini dalam rincian yang mendalam.

Given a multiset S of n (usually non-negative) Integers: {S₁, S₂, ..., S_n} and an Integer W,
the SUBSET-SUM problem asks:
Is there exist a subset I ⊆ {1, 2, ..., n} such that ∑_{i ∈ I} S_i = W?

For example, given n = 5, S = {5, 1, 5, 1, 4}, and W = 7,
then it is a YES-instance with certificate indices {0, 1, 3} or values {5, 1, 1} that sums to 7.

Diberikan n item dinyatakan sebagai pasangan bilangan bulat tak-negatif (w1, v1), (w2, v2), ..., (wn, vn), kapasitas W dan target V, apakah terdapat sebuah subset dari item-item tersebut yang mempunyai berat total tak lebih dari W dan nilai total tidak kurang dari V?

YES-instance: n = 5: {(12, 4), (1, 2), (4, 10), (1, 1), (2, 2)}, W = 15, dan V = 15, sertifikat: ambil semua item kecuali item (12, 4), dengan berat total 8 dan nilai total 15.

NO-instance: menggunakan instance yang sama tetapi V = 16.

Diberikan graf G = (V, E), sebuah subset X ⊆ V dikatakan sebagai set independen jika untuk setiap pasangan simpul u, v ∈ X, maka (u, v) ∉ E.

Diberikan graf G = (V, E), masalah INDEPENDENT-SET (IS) menanyakan: Apakah ada set independen dengan ukuran ≥ k?

Perlu dicatat bahwa kami telah membangun halaman visualisasi mvc khusus yang membahas masalah ini dan berbagai strategi untuk mengatasi masalah ini secara lebih rinci (ingat bahwa satu set simpul adalah IS jika dan hanya jika komplemennya adalah VC).

Halaman ini adalah stub untuk menjelaskan masalah 3-D-MATCHING (3DM).

Halaman ini adalah stub untuk menjelaskan masalah PARTITION-INTO-TRIANGLES (PIT).

Halaman ini adalah stub untuk menjelaskan masalah FEEDBACK-EDGE-SET (FES).

Halaman ini adalah stub untuk menjelaskan masalah SET-COVER (SC).

Diberikan sebuah himpunan T terdiri dari bilangan bulat tak-negatif, apakah kita bisa mempartisi T menjadi dua himpunan dengan jumlah yang sama?

YES-instance: T = [18, 2, 8, 5, 7, 24], sertifikat: S₁ = [18, 5, 7, 2] dan S₂ = [8, 24]
NO-instance: T = [1, 2]

Catatan: Jelas bahwa jika jumlah dari T ganjil, kita tidak bisa mempartisi T menjadi dua himpunan dengan jumlah yang sama (otomatis menjadi NO instance). Tanpa mengurangi sifat umum, masalah PARTITION biasanya dikerjakan untuk instance dengan jumlah dari T adalah genap.

Diberikan sebuah graf G = (V, E), sebuah set dominasi D adalah subset dari simpul-simpul sehingga untuk semua simpulu yang tidak ada di D, ada simpul v di D sedemikian sehingga (u, v) adalah sebuah sisi di G (yaitu, u bersebelahan dengan v).

Masalah keputusan Dominating-Set menanyakan apakah, diberikan sebuah bilangan bulat k, ada sebuah himpunan dominasi di G dengan ukuran paling banyak k.

Diberikan sebuah himpunan S = {S₁, S₂, ..., S_n} yang terdiri dari himpunan, sebuah himpunan H adalah hitting set dari S
jika untuk semua S_i, H ∩ S_i ≠ ∅ (yakni, H mempunyai irisan tidak kosong dengan semua S_i).

Diberikan sebuah himpunan S yang terdiri dari himpunan dan sebuah bilangan bulat tak-negatif k, masalah HITTING-SET (HS) menanyakan:
Apakah terdapat hitting set dari S dengan ukuran ≤ k?.

Contoh: S = {S₁, S₂, S₃, S₄}, S₁ = {2, 3}, S₂ = {6, 7}, S₃ = {1, 4, 5, 7}, S₄ = {3, 7, 8}, k = 2, maka ini adalah YES-instance dengan sertifikat H = {3, 7}.

Reduksi C-SAT ≤p CNF-SAT ditunjukkan di bab 34 CLRS.

Reduksi CNF-SAT ≤p 3-SAT ditunjukkan di bab 34 CLRS.

Halaman ini adalah stub untuk menjelaskan reduksi 3-SAT ≤p CLIQUE.

Halaman ini adalah stub untuk menjelaskan reduksi 3-SAT ≤p SUBSET-SUM.

Apakah anda bisa menyelesaikan rincian dari reduksi waktu-polinomial dan pembuktiannya sendiri?
Cobalah terlebih dahulu sebelum tekan tombol selanjutnya.

Untuk setiap klausa, buat 3 simpul di G, satu untuk setiap literal. Kami menghubungkan ketiga literal dari sebuah klausa menjadi sub-graf segitiga. Kami juga menghubungkan literal ke setiap negasinya (dalam klausa lainnya). Kriteria IS akan memastikan bahwa kita hanya memilih satu variabel per segitiga dan kita tidak akan memilih variabel dalam satu klausa dan negasinya dalam klausa lainnya.

Perhatikan bahwa reduksi ini berjalan dalam waktu-polinomial.

Teorema: YES-instance untuk 3-SAT jika dan hanya jika YES-instance untuk IS.

Bukti: TBA

TBA

Halaman ini adalah stub untuk menjelaskan reduksi CLIQUE ≤p VC.

Halaman ini adalah stub untuk menjelaskan reduksi VC ≤p HC.

TBA

TBA

Ide utama (petunjuk utama) adalah bahwa VC memiliki graf G dengan simpul V dan sisi E, tetapi HC memiliki n himpunan bilangan bulat. Bagaimana jika mengonversi sisi menjadi himpunan berukuran dua?

Ambillah sebuah instance (G = (V, E), k) dari VC.
Untuk tiap sisi e = (u, v), e ∈ E, kita membentuk sebuah himpunan S_e = {u, v} dari HC.
Maka instance HC yang telah dirubah menjadi: ({S_e | e ∈ E}, k).

Catat bahwa reduksi ini berjalan dalam waktu-polinomial, tepatnya O(E).

Dapat mudah dilihat bahwa YES-instance untuk VC jika dan hanya jika YES-instance untuk HC.

Bukti diabaikan: Simpul-simpul C dari VC berhubungan dengan elemen-elemen H dari HS dan sebaliknya.

Ide kuncinya (petunjuk besar) adalah untuk membangun sebuah graf kopmlet G' sehingga HC dalam G merupakan TSP tour biaya minimum dari G'.

Apakah anda bisa menyelesaikan rincian dari reduksi waktu-polinomial dan pembuktiannya sendiri?
Cobalah terlebih dahulu sebelum tekan tombol selanjutnya.

Misalkan G = (V, E) merupakan instance α dari HC. Kita membangun instance β dari TSP sebagai berikut: buatlah sebuah graf komplet G' pada V simpul-simpul yang sama, tetapi untuk setiap pasangan u, v ∈ V: jika u, v ∈ E, maka w(u, v) = 1, dan w(u, v) = 2 (atau nilai apapun yang lebih dari 1) jika tidak.

Catat bahwa reduksi ini berjalan dalam waktu-polinomial, lebih tepatnya O(n²) karena terdapat tidak lebih dari C(n, 2) sisi yand ditambahkan dari G ke G'.

Teorema: G mempunyai Siklus Hamiltonian jika dan hanya jika G' mempunyai jalur TSP dengan biaya tidak lebih dari n.

Bukti: Bagikan menjadi dua bagian:
• (jika) G' mempunyai jalur TSP dengan biaya tidak lebih dari n (YES-instance dari TSP) → G mempunyai Siklus Hamiltonian (YES-instance dari HC)

• (hanya jika) G mempunyai Siklus Hamiltonian (YES-instance dari HC) → G' mempunyai jalur TSP dengan biaya tidak lebih dari n (YES-instance dari TSP)

TBA

The key idea (major hint) is to realize that Independent Set and Vertex Cover are related, one set is the complement of the other set.

Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.

X ⊆ V is a vertex cover of G if and only if V-X is an independent set of G.

Take note that this reduction runs in poly-time, in O(V).

It is easy to see that a YES-instance for IS if and only YES-instance for VC.

Proof → and ← are to be added soon.

TBA

TBA

Ide kunci (petunjuk besar) adalah PARTITION hanya mempunyai n bilangan tetapi KNAPSACK mempunyai n pasangan bilangan bulat. Bagaimana jika kita menduplikatkan bilangan-bilangan? Juga, PARTITION mempunyai nilai target yang spesifik (setengah dari jumlah nilai dari n bilangan) yang juga bisa digunakan sebagai parameter untuk KNAPSACK?

Given a PARTITION instance α with T = [w1, w2, ..., wn] with total sum S = ∑_i=[1..n] w_i, construct a KNAPSACK instance β: {(w1, w1), (w2,w2), ..., (wn,wn)}
with capacity W = S/2 and threshold V = S/2.

Take note that this reduction runs in poly-time, to be precise O(n · log (w_max)) as it just copies n weights to n (weight, weight-as-value) pairs. If we assume w_max fits in standard 32/64-bit signed Integers, then log (w_max)) is just 32/64 respectively and this reduction runs in O(n).

Theorem: YES-instance for PARTITION if and only YES-instance for KNAPSACK.

Proof: Split into two parts:
• YES-instance for PARTITION → YES-instance for KNAPSACK.
• YES-instance for KNAPSACK → YES-instance for PARTITION.