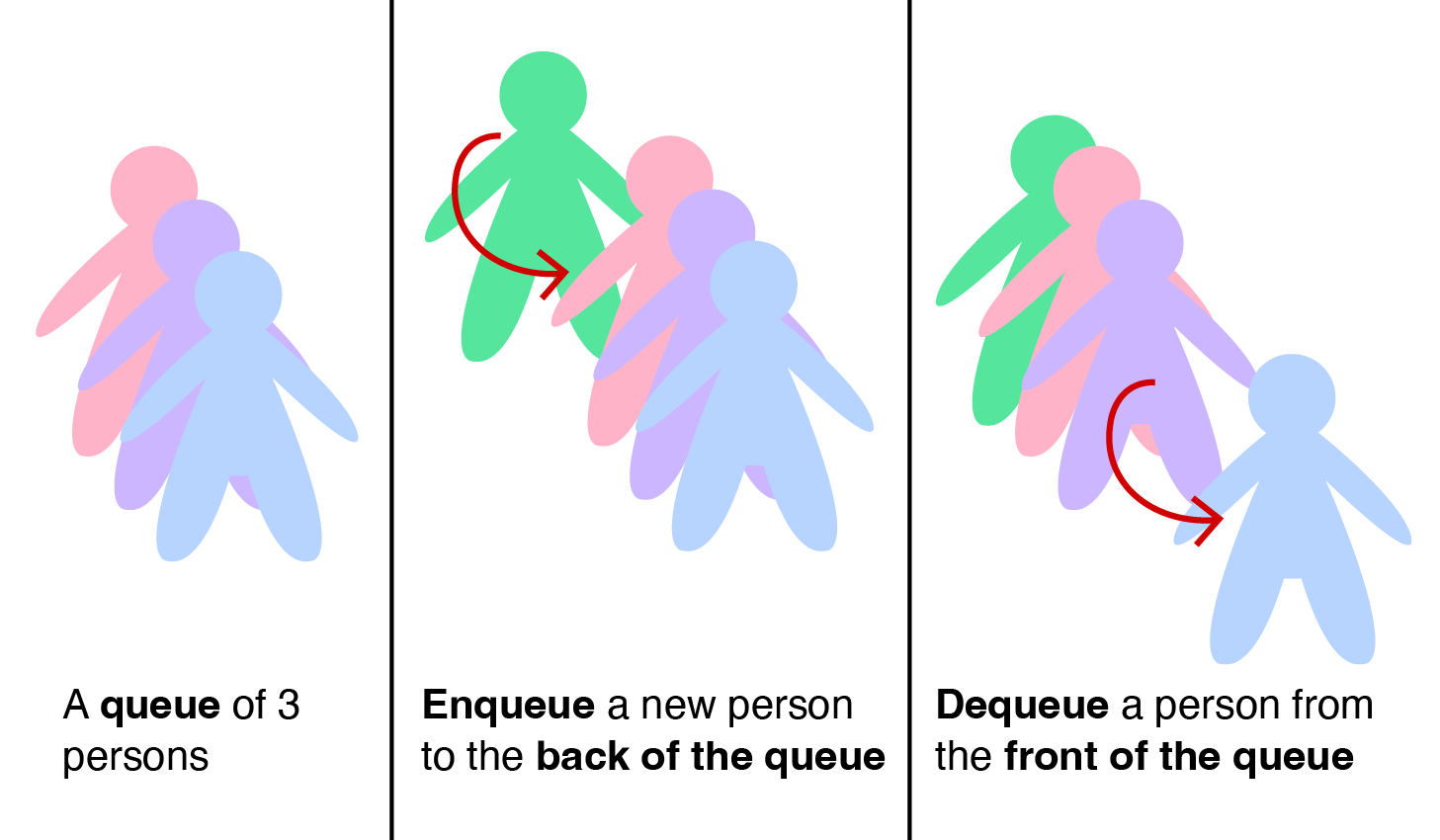
Linked List is a data structure consisting of a group of vertices (nodes) which together represent a sequence. Under the simplest form, each vertex is composed of a data and a reference (link) to the next vertex in the sequence. Try clicking for a sample animation on searching a value in a (Singly) Linked List.
Linked List (and its variations) can be used as the underlying data structure to implement List, Stack, Queue, and Deque ADTs (read this Wikipedia article about ADT if you are not familiar with that term). Another potential data structure that can be used to implement List ADT is (resize-able) array.
In this visualization, we discuss (Singly) Linked List (LL) — with a single next pointer — and its two variants: Stack and Queue, and also Doubly Linked List (DLL) — with both next and previous pointers — and its variant: Deque.
列表是一个项目/数据的序列,其中位置顺序很重要 {a0, a1, ..., aN-2, aN-1}。
常见的列表ADT操作包括:
讨论1:如果我们想从列表中移除具有特定值 v 的项目怎么办?
讨论2:一个列表ADT可以包含重复的项目吗,即,ai = aj 其中 i ≠ j?
Please review (Compact) Array data structure that can also be used to implement List ADT.
For fixed-size collections with known max limit of number of items that will ever be needed, i.e., the max size of M, then array is already a reasonably good data structure for List ADT implementation.
For variable-size collections with unknown size M and where dynamic operations such as insert/remove are common, a simple (fixed-size) array is actually a poor choice of data structure.
For such applications, there are better data structures, including Linked List. Read on...
我们现在介绍链表数据结构。它使用指针/引用使项目/数据在内存中非连续(这是与简单数组的主要区别)。通过指针将项目i与其邻居项目i+1关联,将项目从索引0排序到索引N-1。
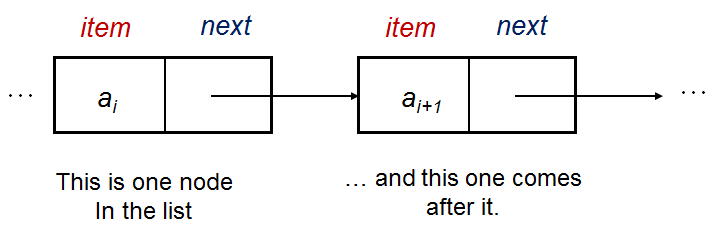
在其基本形式中,链表中的单个顶点(节点)具有这种粗略的结构:
struct Vertex { // 我们可以使用C struct或C++/Python/Java 中的 class
int item; // 数据存储在这里,这个例子中是一个整数
Vertex* next; // 这个指针告诉我们下一个顶点在哪里
};使用默认示例链表 [22 (头)->2->77->6->43->76->89 (尾)] 进行说明,我们有:
a0 其中的 item = 22 和它的 next = a1,
a1 其中的 item = 2 和它的 next = a2,
...
a6 其中的 item = 89 和它的 next = null。
讨论:对于C++实现的链表来说,struct还是class更好?Python或Java实现呢?
我们还在这个链表数据结构中记住了一些额外的数据。我们使用默认示例链表 [22 (头)->2->77->6->43->76->89 (尾)] 进行说明。
就是这样,我们只在数据结构中添加了三个额外的变量。
请注意,许多计算机科学教科书中关于如何实现(单向)链表有各种微妙的差异,例如,是否使用尾指针,是否循环,是否使用虚拟头部项,是否允许重复项 — 参见此幻灯片。
我们在这个可视化中的版本(带有尾指针,非循环,无虚拟头部,不允许重复)可能与你在课堂上学到的内容不完全相同,但基本的思想应该是相同的。
在这个可视化中,每个顶点都有整数项,但这可以根据需要轻松更改为任何其他数据类型。
由于我们只保留头部和尾部指针,需要列表遍历子程序才能到达头部(索引0)和尾部(索引N-1)以外的位置。
由于这个子程序使用频繁,我们将其抽象为一个函数。下面的代码是用C++编写的。
Vertex* Get(int i) { // 返回顶点
Vertex* ptr = head; // 我们必须从头开始
for (int k = 0; k < i; ++k) // 向前推进 i 次
ptr = ptr->next; // 指针指向更高的索引
return ptr;
}它的运行时间为 O(N),因为i可以大到索引N-2。
将此与数组进行比较,我们可以在 O(1) 时间内访问索引 i。
由于链表的性质,比数组版本有更多的情况。
大多数第一次学习链表的计算机科学学生通常在他们的链表代码失败时才意识到所有的情况。
在这个电子讲座中,我们直接详细说明所有的情况。
对于insert(i, v),有四种可能性,即,项目v被添加到:
在头部插入的 (C++) 代码既简单又高效,时间复杂度为 O(1):
Vertex* vtx = new Vertex(); // 从项 v 创建新顶点 vtx
vtx->item = v;
vtx->next = head; // 将这个新顶点链接到(旧的)头顶点
head = vtx; // 新顶点成为新的头部
尝试 ,即 insert(0, 50),在示例链表 [22 (head)->2->77->6->43->76->89 (tail)] 上。
讨论:如果我们使用数组实现来在列表的头部插入,会发生什么?
空的数据结构是一个常见的角落/特殊情况,如果没有适当的测试,往往会导致意外的崩溃。在当前为空的列表中插入新项是合法的,即在索引 i = 0 处。幸运的是,插入头部的同样的伪代码也适用于空列表,所以我们可以像在这个幻灯片中一样使用相同的代码(有一个小改动,我们还需要设置 tail = head)。
尝试 ,即 insert(0, 50),但在空的链表 [] 上。
如果我们也记住尾指针,就像在这个电子讲座中的实现一样(这是建议的,因为它只是一个额外的指针变量),我们可以在尾部项目之后(在i = N)有效地执行插入,时间复杂度为O(1):
Vertex* vtx = new Vertex(); // 这也是一个 C++ 代码
vtx->item = v; // 从项目 v 创建新的顶点 vtx
tail->next = vtx; // 只需链接这个,因为尾部是 i = (N-1)-th 项目
tail = vtx; // 现在更新尾指针
尝试 ,即 insert(7, 10),在示例链表 [22 (head)->2->77->6->43->76->89 (tail)] 上。一个常见的误解是说这是在尾部插入。在尾部元素插入是 insert(N-1, v)。在尾部之后插入是 insert(N, v)。
讨论:如果我们使用数组实现对列表尾部之后的插入会发生什么?
对于 remove(i),有三种(合法)可能性,即,索引 i 是:
讨论:将此幻灯片与插入情况幻灯片进行比较,以了解微妙的差异。从已经为空的链表中删除任何东西是否被认为是'合法'的?
这个案例很直接(用C++编写):
if (head == NULL) return; // 当 SLL 为空时避免崩溃
Vertex* tmp = head; // 这样我们可以稍后删除它
head = head->next; // 记账,更新头指针
delete tmp; // 这是旧的头部
尝试在链表 [22 (head)->2->77->6 (tail)] 上反复使用 。它将一直正确工作,直到链表只包含一个项目,即头部 = 尾部项目。如果 LL 已经为空,我们将阻止执行,因为这是一个非法的情况。
讨论:如果我们使用数组实现来移除列表的头部会发生什么?
我们可以按照以下方式实现链表尾部的移除,假设链表有多于1个项目(在C++中):
Vertex* pre = head;
tmp = head->next;
while (tmp->next != null) // 当邻居不是尾部时
pre = pre->next, tmp = tmp->next;
pre->next = null;
delete tmp; // tmp = (旧) 尾部
tail = pre; // 更新尾部指针
尝试在链表 [22 (头部)->2->77->6 (尾部)] 上反复使用 。它将一直正确工作,直到链表只包含一个项目,头部 = 尾部项目,我们切换到头部移除的情况。如果链表已经为空,我们将阻止执行,因为这是一个非法的情况。
栈是一种特殊的抽象数据类型,其主要操作是向集合添加一个项目,称为推入,只能推入到栈顶,以及从栈顶移除一个项目,称为弹出。
它被称为后进先出(LIFO)数据结构,例如,下面的书堆。
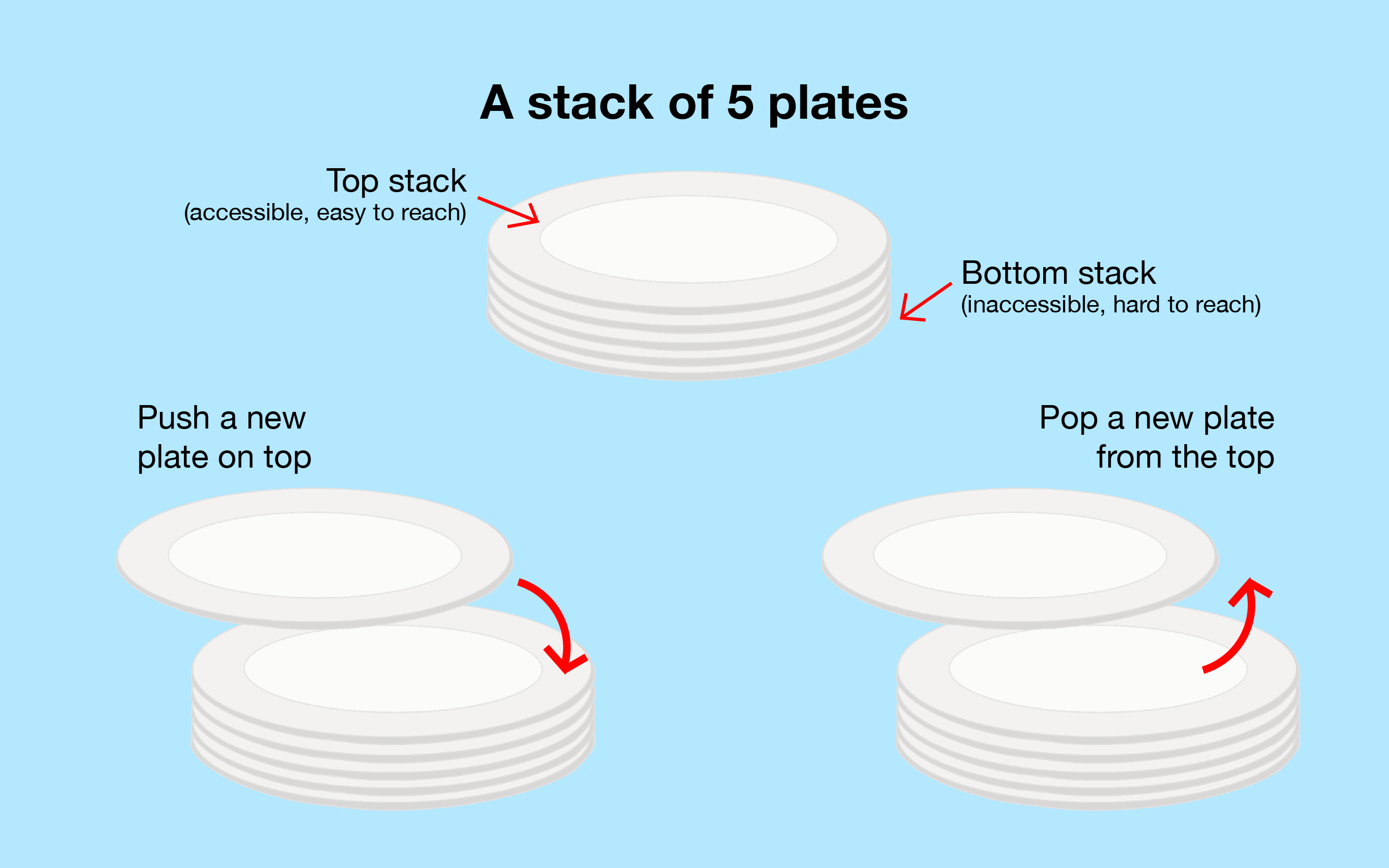
在大多数实现中,以及在这个可视化中,栈基本上是一个受保护的(单向)链表,我们只能查看头部项目,只能向头部推送新项目(在头部插入),例如,尝试 ,并且只能从头部弹出现有项目(从头部移除),例如,尝试 。所有操作都是 O(1)。
在这个可视化中,我们将(单)链表从上到下定向,头/尾项目分别在顶部/底部。在示例中,我们有 [2 (顶部/头部)->7->5->3->1->9 (底部/尾部)]。由于垂直屏幕大小限制(在横向模式下),我们在这个可视化中只允许最多7个项目的栈。
讨论:我们能否使用向量,一个可调整大小的数组,来有效地实现栈ADT?
栈有一些受欢迎的教科书应用程序。一些例子:
数学表达式可能会变得相当复杂,例如,{[x+2]^(2+5)-2}*(y+5)。
括号匹配问题是检查给定输入中的所有括号是否正确匹配的问题,即,( 与 ),[ 与 ] 和 { 与 },等等。
括号匹配对于检查源代码的合法性同样有用。
讨论:事实证明,我们可以使用栈的LIFO行为来解决这个问题。
问题是如何做到这一点?

另一种可能的数组实现方法是通过使用两个索引来避免在出队操作中的项目移动:front(队列最前面的项目的索引,在出队操作后增加)和back(队列最后面的项目的索引,在入队操作后也增加)。
假设我们使用一个大小为M = 8的数组,我们的队列内容如下:[(2,4,1,7),-,-,-,-],其中front = 0(下划线)和back = 3(斜体)。当前活动的队列元素用(绿色)高亮显示。
如果我们调用 dequeue(),我们得到[-,(4,1,7),-,-,-,-],front = 0+1 = 1,和back = 3。
如果我们调用 enqueue(5),我们得到[-,(4,1,7,5),-,-,-],front = 1,和back = 3+1 = 4。
然而,经过许多出队和入队操作后,我们可能会有[-,-,-,-,-,6,2,3],front = 5,和back = 7。到现在为止,尽管数组前面有许多空位,但我们不能再入队任何其他元素。
如果我们允许front和back索引在达到索引M-1时“回绕”到索引0,我们实际上使数组“环形”,并且我们可以使用空位。
例如,如果我们接下来调用 enqueue(8),我们会有[8),-,-,-,-,(6,2,3],front = 5,和back = (7+1)%8 = 0。
然而,这并没有解决固定大小数组实现的主要问题。再进行几次入队操作后,我们可能会得到[8,10,11,12,13),(6,2,3],front = 5,和 back = 4。在这一点上(front = (back+1) % M)),我们不能再入队任何其他东西。
请注意,如果我们知道我们的队列大小永远不会超过固定数组大小M,那么循环数组的想法实际上已经是实现队列ADT的好方法。
然而,如果我们不知道队列大小的上限,我们可以扩大(加倍)数组的大小,例如,使M = 2*8 = 16(两倍大),但这将需要重新复制索引front到back的项目,这是一个慢(但罕见)的O(N)过程,得到[(6,2,3,8,10,11,12,13),-,-,-,-,-,-,-,-,],front = 0,和 back = 7。
PS1:如果你理解摊销分析,这个在循环数组满时的重大O(N)成本实际上可以分摊出来,使得每个入队在摊销意义上仍然是O(1)。
PS2:有一种使用两个栈来实现高效队列的替代方法。怎么做呢?
如果我们真的不知道队列大小的上限,那么单链表(SLL)可以是实现队列ADT的一个好的数据结构。
回想一下,在队列中,我们只需要列表的两个极端端点,一个只用于插入(入队),一个只用于移除(出队)。
如果我们回顾这张幻灯片,我们会看到在单链表中在尾部插入和从头部移除都很快,即,O(1)。因此,我们将单链表的头/尾指定为队列的前/后。然后,由于链表中的项目不是在计算机内存中连续存储的,我们的链表可以根据需要进行增长和缩小。
在我们的可视化中,队列基本上是一个受保护的单链表,我们只能查看头部项目,将新项目入队到当前尾部之后的一个位置,例如,尝试 ,并从头部出队现有项目,例如,尝试 (这本质上是一个出队操作)。所有操作都是O(1)。
在单链表中,即使我们通过尾指针直接访问尾元素,删除尾元素的主要问题是,我们必须在此类删除后更新尾指针,使其指向尾部之前的一个元素。
有了双链表向后移动的能力,我们可以通过tail->prev找到尾部之前的这个元素...因此,我们可以这样实现尾部的删除(在C++中):
Vertex* tmp = tail; // 记住尾部项
tail = tail->prev; // 实现 O(1) 性能的关键步骤 :O
tail->next = null; // 删除这个悬空的引用
delete tmp; // 删除旧的尾部
现在这个操作是 O(1)。尝试在示例 DLL [22 (head)<->2<->77<->6<->43<->76<->89 (tail)] 上使用 。
创建操作对所有五种模式都是相同的。
然而,五种模式之间的搜索/插入/删除操作有些微小的差异。
对于栈,您只能从顶部/头部进行 peek/限制搜索,push/限制插入,和 pop/限制删除。
对于队列,您只能从前端(或有时是后端)进行 peek/限制搜索,从后端 push/限制插入,和从前端 pop/限制删除。
对于双端队列,您可以从前端/后端进行 peek/限制搜索,enqueue/限制插入,dequeue/限制删除,但不能从中间进行。
单向(单链)和双向链表没有这样的限制。
以下是关于链表的更高级的见解:
关于这个数据结构的一些更有趣的问题,请在链表培训模块上练习。
我们还有一些编程问题,这些问题在一定程度上需要使用链表,栈,队列或双端队列这些数据结构:
UVa 11988 - Broken Keyboard (又名 Beiju Text),
Kattis - backspace,和
Kattis - integerlists。
尝试它们以巩固和提高你对这种数据结构的理解。如果这可以简化你的实现,你可以使用 C++ STL,Python 标准库,或 Java API。