Sebuah Timbunan Biner (Maks(imum)) (Binary (Max) Heap) adalah pohon biner komplet yang menjaga properti Timbunan Maks.
Timbunan Biner adalah salah satu struktur data yang dapat digunakan sebagai implementasi Tipe Data Abstrak (Abstract Data Type, ADT) Antrean Berprioritas (Priority Queue, PQ). Dalam sebuah PQ, setiap elemen mempunyai "prioritas" dan sebuah elemen dengan prioritas yang lebih tinggi akan diproses terlebih dahulu sebelum elemen dengan prioritas yang lebih rendah (elemen-elemen dengan prioritas yang sama akan diurutkan berdasarkan aturan Pertama-Datang Pertama-Keluar (First-In First-Out, FIFO) seperti Antrean (Queue) normal). Cobalah kilk untuk animasi contoh tentang meng-ekstrak nilai maks dari sebuah Timbunan Biner acak diatas.
Untuk memperkecil fokus diskusi kita, visualisasi ini didesain untuk menampilkan Timbunan Biner Maks yang berisi bilangan bulat dimana duplikat-duplikat diperbolehkan. Lihat ini untuk konversi mudah ke Timbunan Biner Min. Seceara umum, objek lainnya yang bisa dibandingkan bisa disimpan dalam sebuah Timbunan Biner Maks (seperti Timbunan Biner Maks terdiri dari floating point, dll).
Pohon Biner Komplet: Setiap level di pohon biner, kecuali mungkin level terakhir/terbawah, sepenuhnya terisi, dan semua simpul-simpul di level terakhir berada di sisi paling kiri sebisa mungkin.
Properti Timbunan Biner Maks: Orang tua (parent) dari setiap simpul - kecuali mungkin akarnya - berisi nilai lebih besar dari nilai dari simpul tersebut. Ini adalah definisi yang lebih-mudah-diverifikasi daripada definisi alternatif ini: Nilai dari setiap simpul - kecuali mungkin daun/dedaunan - harus lebih besar dari nilai dari satu (atau kedua) anak(-anak)nya.
Tipe Data Abstrak (Abstract Data Type, ADT) Antrean Berprioritas (Priority Queue, PQ) mirip dengan ADT Antrean (Queue) normal, tetapi dengan dua operasi-operasi penting berikut:
Bayangkan: Anda adalah Pengatur Lalu Lintas Udara (Air Traffic Controller, ATC) yang bekerja di sebuah menara kontrol dari sebuah bandara.
Anda telah menjadwalkan pesawat X/Y untuk mendarat di 3/6 menit berikutnya. Keduanya memiliki bahan bakar yang cukup untuk setidaknya 15 menit kedepan dan keduanya hanya 2 menit jauhnya dari bandara anda. Anda mengamati bahwa jalur pacu bandara anda saat ini kosong.
Jika anda tidak tahu, sebuah pesawat dapat diinstruksikan untuk terbang dalam pola statis (holding pattern) dekat sebuah bandara sampai waktu pendaratan yang sudah dijadwalkan.
Anda harus menghadiri kuliah nyata untuk mengetahui apa yang terjadi selanjutnya...
Akan ada dua pilihan yang akan ditampilkan kepada anda dan anda harus memutuskan:
Jika kedua opsi tersebut tidak masuk akal buat anda, anda tidak perlu melakukan apa-apa.
Ada beberapa penggunaan-penggunaan potensial dari ADT PQ dalam kehidupan nyata selain apa yang anda baru saja lihat (hanya di kuliah nyata).
Diskusi: Bisakah anda menyebutkan beberapa situasi-situasi kehidupan nyata lainnya dimana sebuah PQ dibutuhkan?
Kita bisa mengimplementasikan ADT PQ ini menggunakan larik (sirkular) atau Senarai Berantai (Linked List) tetapi kita akan mendapatkan operasi Enqueue atau Dequeue yang pelan (yaitu dalam O(N)).
Diskusi: Kenapa?
Sekarang, mari lihat visualisasi dari sebuah Timbunan Biner Maks(imum) (acak) diatas. Anda akan melihat sebuah pohon biner komplit dan seluruh simpulnya kecuali akarnya memenuhi properti timbunan maks (A[parent(i)] > A[i] — yang tetap baik-baik saja meskipun ada bilangan-bilangan bulat yang terduplikasi).
Anda bisa di antara format pohon biner komplit yang lebih intuitif atau larik padat yang mendasari implementasi Timbunan Biner (Maks).
Quiz: Based on this Binary (Max) Heap property, where will the largest integer be located?
Fakta penting untuk dihafal saat ini: Jika kita memiliki Timbunan Biner dengan N elemen, tingginya tidak akan lebih tinggi dari O(log N) karena kita akan menaruhnya sebagai pohon biner komplet.
Analisa sederhana: Besarnya N dari sebuah pohon biner penuh (lebih dari sekedar komplet) dengan tinggi h adalah selalu N = 2(h+1)-1, sehingga h = log2(N+1)-1 ~= log2 N.
Lihat contoh diatas dengan N = 7 = 2(2+1)-1 or h = log2(7+1)-1 = 2.
Fakta ini penting untuk analisa dari semua operasi-operasi yang berhubungan dengan Timbunan Biner.
Sebuah pohon biner komplet dapat disimpan dengan efisien sebagai larik padat A karena tidak ada bolong diantara simpul-simpul dari sebuah pohon biner komplet maupun elemen-elemen dari larik padat. Untuk memudahkan operasi-operasi navigasi dibawah, kami menggunakan larik berbasis-1. VisuAlgo menunjukkan indeks dari setiap simpul sebagai label merah dibawah setiap simpul. Baca indeks-indeks tersebut secara terurut dari 1 sampai N, maka anda akan melihat simpul-simpul dari pohon biner komplet dari atas ke bawah, kiri ke kanan. Untuk membantu anda mengerti ini, beberapa kali.
Dengan cara ini, kita bisa mengimplementasikan operasi-operasi penjelajahan pohon biner standar dengan manipulasi-manipulasi indeks sederhana (dengan bantuan manipulasi penggeseran bit):
Tips Pro: Cobalah buka dua kopi dari VisuAlgo pada dua jendela browser. Cobalah visualisasikan Timbunan Biner Maks yang sama dalam dua mode yang berbeda dan bandingkan.
Dalam visualisasi ini, anda dapat melakukan beberapa operasi umum Timbunan Biner (Maksimum):
Terdapat operasi-operasi Timbunan Biner (Maksimum) lain, namun saat ini kami tidak menunjukkannya untuk alasan pedagogis beberapa modul NUS.
Apakah anda mengerti kenapa memulai dari tempat pemasukan (indeks N+1) keatas (sampai maksimum simpul akar) dan menukar sebuah simpul dangan orang tuanya ketika terjadi pelanggaran properti Timbunan Maks selama pemasukkan adalah sebuah strategi yang benar?
Kompleksitas waktu dari operasi Masukkan(v) ini adalah O(log N).
Diskusi: Apakah anda mengerti penurunannya?
EkstrakMaks(): Pelaporan dan penghapusan nilai maksimum (akar) dari Timbunan Biner Maks memerlukan sebuah elemen lain untuk menggantikannya, karena jika tidak, maka Timbunan Biner Maks (sebuah pohon biner komplit, atau 林/Lín dalam bahasa Mandarin/pohon) menjadi dua sub-pohon yang terpisah (dua kopi dari 木/mù dalam bahasa Mandarin/kayu). Elemen tersebut harus merupakan indeks terakhir N dengan alasan yang sama: Untuk menjaga properti larik padat (compact) = pohon biner komplet.
Karena kita mempromosikan sebuah simpul daun menjadi simpul akar dari sbeuah Timbunan Biner, properti Timbunan Maks dapat dilanggar dengan mudah. Operasi EkstraksMaks() ini lalu membetulkan kembali properti tersebut mulai dari akar ke bawah dengan membandingkan nilai saat ini dengan anak-anaknya/yang lebih besar (bila perlu). Sekarang cobalah pada Timbunan Biner (Maks) yang ditunjukkan saat ini.
Operasi membetulkan properti Timbunan Maks kebawah tidak memiliki nama standar. Kami menyebutnya ShiftDown tetapi orang-orang lain mungkin menyebutnya sebagai operasi BubbleDown atau Heapify.
Kenapa jika sebuah simpul memiliki dua anak, kita harus mengecek (dan mungkin menukar) simpul tersebut dengan anak yang lebih besar saat membereskan properti Timbunan Maks kebawah?
Kenapa kita tidak bisa membandingkan dengan simpul kiri (atau kanan, jika ada) saja?
Kompleksitas waktu dari operasi EkstrakMaks() ini adalah O(log N).
Diskusi: Apakah anda mengerti penurunannya?
Sampai pada saat ini, kita telah memiliki struktur data yang bisa mengimplementasikan kedua operasi-operasi penting dari ADT Antrean Berprioritas (Priority Queue, PQ) secara efisien:
Tetapi, kita sebenarnya bisa melakukan beberapa operasi-operasi lainnya dengan Timbunan Biner.
Buat(A): Membuat sebuah Timbunan Biner (Maks) valid dari array masukan A dengan N integer (dipisahkan dengan koma) ke dalam Timbunan Biner Maks kosong.
Ada dua varian untuk operasi ini, versi sederhana dalam O(N log N) dan versi advanced yang berjalan dalam O(N).
Pro Tip: Cobalah buka dua jendela VisuAlgo di browser anda. Jalankan kedua varian operasi Buat(A) pada kasus terburuk 'Contoh terurut' untuk melihat perbedaan mencolok dari keduanya.
Analisa: Sebuah analisa longgar menghasilkan O(N/2 log N) tetapi ini hanyalah O(2*N) = O(N) — selebihnya di sini. . Sekarang dari array masukan A=[1,2,3,4,5,6,7] dan lihat pada kasus terburuknya, operasi ini jauh lebih baik dibandingkan versi O(N log N).
Pembuktian sederhana tentang mengapa separuh dari Timbunan Biner (Maks) dengan N (tanpa kehilangan makna umum, mari asumsikan bahwa N adalah genap) elemen adalah dedaunan adalah sebagai berikut:
Misalkan daun terakhir berada pada indeks N, maka orang tua dari daun terakhir tersebut ada di indeks i = N/2 (ingat slide ini). Anak kiri dari simpul i+1, jika ada (sesungguhnya tidak ada), adalah 2*(i+1) = 2*(N/2+1) = N+2, yang sudah lebih besar dari indeks N (daun terakhir) jadi indeks i+1 pasti juga adalah sebuah simpul daun yang tidak mempunyai anak. Karena indeks-indeks dari Timbunan Biner beruruta, pada dasarnya indeks-indeks [i+1 = N/2+1, i+2 = N/2+2, ..., N], yaitu separuh dari seluruh simpul-simpul, adalah dedaunan.
Analisa Sederhana: HeapSort() dengan jelas berjalan dalam O(N log N) — sebuah algoritma pengurutan berbasis perbandingan yang optimal.
Meskipun HeapSort() berjalan dalam waktu θ(N log N) untuk semua kasus (terbaik/rata-rata/terjelek), apakah Heap Sort benar-benar algoritma berbasis-pembandingan terbaik?
Diskusi: Bagaimana dengan performa caching dari HeapSort()?
Anda telah mencapai akhir dari bahan-bahan dasar dari struktur data Timbunan Biner (Maks) dan kami menyemangati anda untuk mengeksplorasi lebih lanjut dalam Mode Eksplorasi.
Tetapi, kami masih memiliki beberapa tantangan-tantangan menarik untuk anda tentang Timbunan Biner (Maks) yang akan kami sebutkan di bagian ini.
Ketika anda telah menyelesaikan semuanya, kami mengundang anda untuk mempelajari algoritma-algoritma yang lebih lanjut yang menggunakan Antrean Berprioritas sebagai (salah satu dari) struktur datanya, seperti algoritma MST Prim, algoritma SSSP Dijkstra, algoritma pencarian A* (belum ada di VisuAlgo), dan beberapa algoritma-algoritma berbasis-greedy lainnya, dsb.
Sebelumnya, kita telah melihat bahwa kita bisa membuat Timbunan Biner Maks dari sebuah larik acak dengan N elemen dalam O(N) daripada O(N log N). Sekarang, kita akan menganalisa kompleksitas waktu ini.
Pertama, ingatlah bahwa ketinggian dari sebuah pohon biner komplet berukuran N adalah log2 N.
Kedua, perhatikan bahwa harga untuk menjalankan operasi shiftDown(i) bukanlah batas kotor O(log N), tetapi O(h) dengan h menyatakan tinggi subtree berakar di i.
Ketiga, terdapat ceil(N/2h+1) simpul di ketinggian h dalam sebuah pohon biner komplet.
Dari contoh pohon biner komplet di atas dengan N = 7 dan h = 2, terdapat:
ceil(7/20+1) = 4 simpul: {44,35,26,17} di ketinggian h = 0,
ceil(7/21+1) = 2 simpul: {62,53} di ketinggian h = 1, dan
ceil(7/22+1) = 1 simpul: {71} di ketinggian h = 2.
Harga dari Buat(A), versi O(N) merupakan:
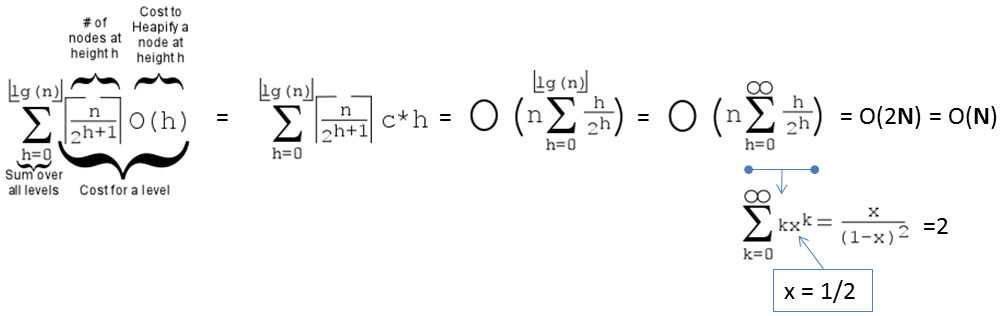
Catanan: Jika formulanya terlalu rumit, seorang murid modern bisa menggunakan WolframAlpha.
Pembuatan Timbunan Maks dengan kompleksitas lebih cepat O(N) dari sebuah larik acak N elemen sangat penting untuk mendapatkan solusi lebih cepat jika kita ingin mendapatkan K elemen terbesar dari N elemen, yakni PartialSort().
Setelah pembuatan Timbunan Maks dalam O(N), kita bisa memanggil operasi O(log N) ExtractMax() K kali untuk mendapatkan K elemen terbesar dalam Timbunan Biner Maks. Sekarang, cobalah pada Timbunan Biner Maks yang ditunjukkan.
Analisis: PartialSort() jelas berjalan dalam O(N + K log N) — algoritma yang sensitif dengan output, yakni kompleksitas waktu berhubungan dengan ukuran keluaran K. Ini lebih cepat daripada batas bawah O(N log N) jika kita mengurutkan semua N elemen jika K < N.
Jika kita hanya berurusan dengan angka-angka (termasuk dalam visualisasi ini yang dibatasi nya untuk bilangan-bilangan bulat saja), maka mudah untuk mengkonversi Timbunan Biner Maks ke Timbunan Biner Min tanpa mengubah apapun, dan sebaliknya.
Kita dapat membuat ulang Timbunan Biner dengan menegasi (mengalikan dengan -1) setiap bilangan bulat di Timbunan Biner asli. Jika kita mulai dengan Timbunan Biner Maks, maka Timbunan Biner yang dihasilkan adalah Timbunan Biner Min (jika kita tidak memperdulikan simbol-simbol negatif — lihat gambar diatas), dan sebaliknya.
Untuk beberapa aplikasi-aplikasi Antrean Berprioritas (misalkan HeapDecreaseKey dalam algoritma Dijkstra), kita mungkin harus memodifikasi (menaikkan atau menurunkan) prioritas dari sebuah nilai yang sudah dimasukkan kedalam Timbunan Biner (Maks). Jika indeks i dari nilai tersebut diketahui, kita dapat menggunakan strategi mudah sebagai berikut: Mutakhirkan saja A[i] = newv dan lalu kita memanggil kedua shiftUp(i) dan shiftDown(i). Hanya maksimum satu dari operasi restorasi properti Timbunan Maks yang akan berhasil, yaitu shiftUp(i)/shiftDown(i) akan dijalankan jika newv >/< nilai lama dari A[parent(i)]/A[larger of the two children of i], masing-masing.
Sehingga, PerbaruiKunci(i, vbaru) bisa dilakukan dalam O(log N), asal saja kita mengetahui indeks i.
Untuk beberapa aplikasi-aplikasi Antrean Berprioritas, kita mungkin harus menghapus nilai yang sudah ada yang telah dimasukkan kedalam Timbunan Biner (Maks) (dan nilai ini kebetulan bukan akar). Sekali lagi, jika indeks i dari nilai tersebut diketahui, kita bisa melakukan strategi muda berikut ini: Mutakhirkan saja A[i] = A[1]+1 (sebuah angka besar yang lebih besar dari akar saat ini), panggil shiftUp(i) (secara teknis, PerbaruKunci(i, A[1]+1)). Ini akan membawa indeks i menjadi akar yang baru, dan dari situ, kita dapat dengan mudah memanggil EktraksMax() sekali untuk menghapusnya.
Maka, Hapus(i) bisa dilakukan dalam O(log N), jika kita mengetahui indeks i.
Diskusi: Sekarang untuk PerbaruiKunci(i, vbaru) dan Hapus(i), apa yang terjadi jika kita diberikan vlama dan oleh karena itu kita harus mencari lokasinya di Timbunan Biner (Maks)? Bisakah kita melakukan ini lebih cepat dari O(N)?
Jika ada kunci duplikat, implementasi standar Binary Heap seperti yang ditunjukkan dalam visualisasi ini tidak menjamin stabilitas. Sebagai contoh, jika kita menyisipkan tiga salinan {7, 7, 7}, misalnya, {7a, 7b, dan 7c} (akhiran a, b, c hanya ada untuk kejelasan), dalam urutan itu, ke dalam Binary (Max) Heap yang awalnya kosong. Kemudian, saat ekstraksi pertama, root (7a) akan diekstraksi terlebih dahulu dan daun terakhir yang ada (7c) akan menggantikan 7a. Karena 7c dan 7b (tanpa akhiran) sama (7 dan 7), tidak ada pertukaran yang terjadi dan sehingga ekstraksi maksimum kedua akan mengambil 7c alih-alih 7b terlebih dahulu — not stable.
Jika kita benar-benar perlu menjamin stabilitas elemen yang sama, kita mungkin perlu melampirkan akhiran berbeda seperti yang ditunjukkan sebelumnya untuk membuat elemen-elemen identik tersebut menjadi unik lagi.
Jika anda mencari implementasi dari sebuah Timbunan Biner (Maks) untuk mendapatkan Antrean Berprioritas (Priority Queue), maka ada berita baik.
C++ dan Java sudah memiliki implementasi-implementasi Antrean Berprioritas built-in yang sangat mungkin menggunakan struktur data ini. Mereka adalah C++ STL priority_queue (secara default adalah Antrean Berprioritas Maks) dan Java PriorityQueue (secara default adalah Antrean Berprioritas Min). Tetapi, implementasi built-in mungkin tidak cocok untuk melakukan beberapa operasi-operasi PQ tambahan (detilnya tidak disebut untuk alasan pedagogis di sebuah modul NUS).
Python heapq juga ada tetapi performanya cukup pelan. OCaml tidak mempunyai Antrean Berprioritas built-in tetapi kita bisa menggunakan sesuatu yang lain yang akan disebut di modul-modul lain di VisuAlgo (alasan kenapa detail-detailnya dirahasiakan sama seperti diatas).
Catatan: Heap Sort sangat mungkin dipakai dalam algoritma C++ STL partial_sort.
Tetapi, inilah implementasi kami tentang BinaryHeapDemo.cpp | py | java.
Untuk beberapa pertanyaan-pertanyaan menarik tentang struktur data ini, silahkan coba latihan pada modul latihan Timbunan Biner (login tidak dibutuhkan).
Tetapi untuk murid-murid NUS, anda sebaiknya login menggunakan akun kelas resmi anda, secara ofisial menyelesaikan modul ini, dan penghargaan tersebut akan dicatat di akun pengguna anda.
Kita juga memiliki beberapa masalah-masalah pemrograman yang membutuhkan penggunaan struktur data Timbunan Biner ini: UVa 01203 - Argus dan Kattis - numbertree.
Cobalah mereka untuk mengkonsolidasikan dan meningkatkan pemahaman anda tentang struktur data ini. Anda diijinkan untuk menggunakan C++ STL priority_queue, Python heapq, atau Java PriorityQueue jika itu mempermudah implementasi anda.
Setelah menghabiskan satu kuliah panjang tentang Timbunan Biner (Maks), pernyataan berikutnya bisa mengejutkan anda...
Timbunan Biner (Maks) mungkin bukan struktur data terbaik untuk mengimplementasikan (beberapa operasi-operasi spesifik) dari ADT Antrian Berprioritas...
Diskusi: Jadi apakah data struktur alternatifnya?