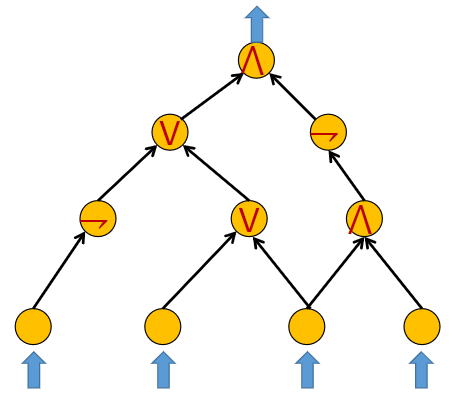
 YES-instance (Sample certificate: False, True, True, False)
YES-instance (Sample certificate: False, True, True, False)A reduction is a way of transforming/converting one problem into another problem.
Suppose you have a problem A which you do not know how to solve. However, you know an algorithm to solve problem B. If you can "transform" an instance α of problem A into an instance β of problem B, you can use the known algorithm for B to solve the "transformed" instance β, and obtain the solution for α from the solution β, by "reversing the transformation". We then say that A reduces to B.
Through reductions, we have another tool to solve problems.
Furthermore, with an efficient, polynomial-time "transformation", reductions provide the ability to compare the "hardness" of two problems A and B.
Given two decision problems A and B, a polynomial-time reduction from A to B,
denoted A ≤p B, is a transformation from instance α of A to instance β of B such that:
With a polynomial-time reduction, we will be able to claim:
If B is "easily solvable", then so is A.
If A is "hard", then so is B.
However, if B is "hard", it does not imply that A is "hard".
Likewise, if A is "easy", it does not mean that B is "easy".
In this (static) visualization page (no animation), we want to show the (well-known) network of reductions from different NP-complete decision problems to another. In theory, since all these problems are NP-complete, they can all be reduced to one another, but the transformation can become very convoluted for some problems.
This network of reductions shown in this page is a combination from "Introductions to Algorithms (CLRS, 4th edition)", Karp's 21 NP-complete problems, "Computers and Intractability (Garey and Johnson, 79), etc.
The content of this visualization will be added over time as more and more NP-complete problems are discussed in NUS algorithm classes.
A vertex contains the (abbreviated) name of an NP-complete decision problem. Hover over it to see its full name. You can also click on the vertex to open the relevant slide that formally describes the problem.
A directed edge between vertices opens the slide which contains the proof of reduction from one problem to the other, in the direction of the arrow, as found in many computational complexity resources (books/Internet/etc). The reduction proof is generally if and only if (iff). Green arrow indicates that we have digitize the reduction proof. Black arrow indicates that we have not done so. We hope to add as much content to this page gradually over time.
The CIRCUIT-SATISFIABILITY problem (C-SAT) is the decision problem of determining whether a given Boolean circuit - essentially a Directed Acyclic Graph - (using AND ∧, OR ∨, NOT ¬ gates) has an assignment of its n binary inputs that makes the output True (1). In other words, it asks whether the n inputs to a given Boolean circuit can be consistently set to True (1) or False (0) such that the circuit outputs True (1). If that is the case, the circuit is called satisfiable. Otherwise, the circuit is called unsatisfiable.
 YES-instance (Sample certificate: False, True, True, False)
YES-instance (Sample certificate: False, True, True, False)
Important: L ≤p C-SAT for every language L ∈ NP.
Definitions: Literal is a Boolean variable or its negation, e.g., xi, x̄i.
Clause: A disjunction (OR ∨) of literals, e.g, Cj = x1 ∨ x̄2 ∨ x3.
The CONJUNCTIVE-NORMAL-FORM-SATISFIABILITY (CNF-SAT), or sometimes just called as SATISFIABILITY (SAT) problem, is the decision problem of determining whether a given formula Φ that is conjunction (AND ∧) of clauses, e.g., Φ = C1 ∧ C2 ∧ C3 ∧ C4, has a satisfying truth assignment.
3-CNF-SAT(isfiability), usually just called as 3-SAT problem, is a CNF-SAT where each clause contains exactly 3 literals corresponding to different variables.
Example: Φ = (x̄1 ∨ x2 ∨ x3) ∧ (x1 ∨ x̄2 ∨ x3) ∧ (x̄1 ∨ x2 ∨ x4) is a YES-instance.
(Sample certificate: x1 = x2 = x4 = True, x3 = False).
A clique is a set of vertices C of graph G = (V, E) such that ∃ an edge between every pair of distinct vertices in the set (u, v ∈ C, ∃ (u, v)). Set C is a complete subgraph of G. Then the size of the clique is the number of vertices in the set C.
The CLIQUE decision problem asks the following question on a graph G = (V, E):
Does there exist a complete subgraph in G of at least size k?
Given a graph G = (V, E), a subset C ⊆ V is said to be a vertex cover if for each edge (u, v) ∈ E, either u ∈ C and/or v ∈ C.
Given a graph G = (V, E), the VERTEX-COVER (VC) problem asks:
Does there exist a vertex cover of size ≤ k?
Note that we have built a specialized mvc visualization page that discusses this problem and various strategies to attack this problem in a much detailed manner.
Given an undirected unweighted graph G = (V, E),
the HAMILTONIAN-CYCLE (HC, sometimes abbreviated as HAM-CYCLE) problem asks:
Does there exist a (simple) cycle passing through all vertices exactly once?
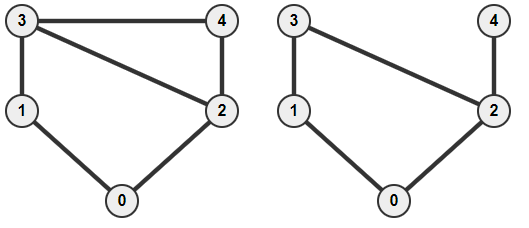
Left/YES-instance (Sample certificate: 0-1-3-4-2-0) ------- ------- ------- Right/NO-instance
Given an undirected complete graph with non-negative weight on edges and b ∈ R+,
the TRAVELING-SALESPERSON(/previously MAN)-PROBLEM (TSP) problem asks:
Does there exist a tour of cost at most b?
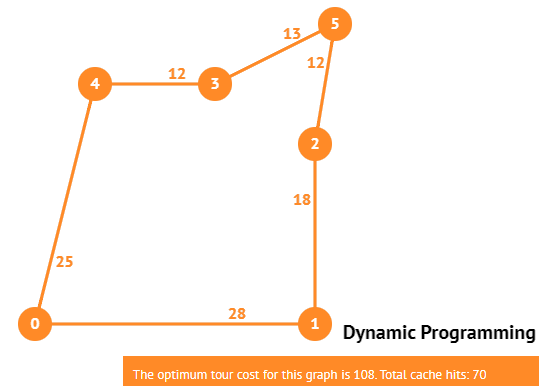
YES-instance for b = 108 but NO-instance for b = 107 as OPT = 108
Note that we have built a specialized tsp visualization page that discusses this problem and various strategies to attack this problem in a much detailed manner.
Given a multiset S of n (usually non-negative) Integers: {S1, S2, ..., Sn} and an Integer W,
the SUBSET-SUM problem asks:
Is there exist a subset I ⊆ {1, 2, ..., n} such that ∑i ∈ I Si = W?
For example, given n = 5, S = {5, 1, 5, 1, 4}, and W = 7,
then it is a YES-instance with certificate indices {0, 1, 3} or values {5, 1, 1} that sums to 7.
Given n items described by non-negative Integer pairs (w1, v1), (w2, v2), ..., (wn, vn), capacity W and threshold V, is there a subset of item with total weight at most W and total value at least V?
YES-instance: n = 5: {(12, 4), (1, 2), (4, 10), (1, 1), (2, 2)}, W = 15, and V = 15, certificate: take everything except item (12, 4) with total weight 8 and total value 15.
NO-instance: use the same instance as above but V = 16.
Given a graph G = (V, E), a subset X ⊆ V is said to be an independent set if for each pair of vertices u, v ∈ X, then (u, v) ∉ E.
Given a graph G = (V, E), the INDEPENDENT-SET (IS) problem asks:
Does there exist an independent set of size ≥ k?
Note that we have built a specialized mvc visualization page that discusses this problem and various strategies to attack this problem in a much detailed manner (remember that a set of vertices is IS if and only if its complement is a VC).
This page is a stub to explain 3-D-MATCHING (3DM) problem.
This page is a stub to explain PARTITION-INTO-TRIANGLES (PIT) problem.
This page is a stub to explain FEEDBACK-EDGE-SET (FES) problem.
This page is a stub to explain SET-COVER (SC) problem.
Given a set T of non-negative Integers, can we partition T into two sets of equal sum?
YES-instance: T = [18, 2, 8, 5, 7, 24], certificate: S1 = [18, 5, 7, 2] and S2 = [8, 24]
NO-instance: T = [1, 2]
PS: Obviously if the sum of T is odd, we cannot partition T into two sets with equal sum (immediately a NO instance). Without loss of generality, PARTITION problem is usually asked on instances when the sum of T is even.
Given a graph G = (V, E), a dominating set D is a subset of vertices such that for all other vertices u that are not in D, there exists some vertex v in D such that (u, v) is an edge in G (i.e., u is adjacent to v).
The Dominating-Set decision problem asks if given an integer k, there exists a dominating set in G of at most size k.
Given a set of sets S = {S1, S2, ..., Sn}, a set H is said to be a hitting set of S
if for all Si, H ∩ Si ≠ ∅ (i.e., H has a non-empty intersection with all Si).
Given the set of sets S and a non-negative integer k, the HITTING-SET (HS) problem asks:
Is there exists a hitting set of S of size ≤ k?.
Example: S = {S1, S2, S3, S4}, S1 = {2, 3}, S2 = {6, 7}, S3 = {1, 4, 5, 7}, S4 = {3, 7, 8}, k = 2, then it is a YES-instance with certificate H = {3, 7}.
C-SAT ≤p CNF-SAT reduction is shown in CLRS Chapter 34.
CNF-SAT ≤p 3-SAT reduction is shown in CLRS Chapter 34.
This page is a stub to explain 3-SAT ≤p CLIQUE reduction.
This page is a stub to explain 3-SAT ≤p SUBSET-SUM reduction.
The key idea (major hint) is that 3-CNF-SAT has k clauses (disjunction of 3 literals) but IS is on a graph G = (V, E). How about creating k triangles (with 3 vertices = 3 literals each) and do something involving a variable and its negation.
Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.
For each clause, create 3 vertices in G, one for each literal.
We connect these 3 literals of a clause into a triangle sub-graph.
We also connect a literal to each of its negation (in any other clauses).
The IS criteria will ensure that we will only pick exactly one variable per triangle and we will not pick a variable in one clause and its negation in any other clause.
Take note that this reduction runs in poly-time.
Theorem: YES-instance for 3-SAT if and only YES-instance for IS.
Proof: To be added.
To be added
This page is a stub to explain CLIQUE ≤p VC reduction.
This page is a stub to explain VC ≤p HC reduction.
To be added
To be added
The key idea (major hint) is to that VC has a graph G with V vertices and E edges but HC has n sets of Integers. How about converting the edges into sets of size two?
Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.
Take an instance (G = (V, E), k) of VC.
Then for each edge e = (u, v), e ∈ E, we create a set Se = {u, v} of HC.
Thus the transformed instance of HC is: ({Se | e ∈ E}, k).
Take note that this reduction runs in poly-time, in O(E).
It is easy to see that a YES-instance for VC if and only YES-instance for HC.
Proof omitted: The vertices in C of VC correspond to elements in H of HS and vice versa.
The key idea (major hint) is to build a weighted complete graph G' such that the HC in G turns out to be the least cost tour in G'.
Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.
Let G = (V, E) be an instance α of HC. We build an instance β of TSP as follows: create a complete graph G' on the same V vertices, but for each pair u, v ∈ V: if u, v ∈ E, then w(u, v) = 1, else w(u, v) = 2 (or anything greater than 1).
Take note that this reduction runs in poly-time, to be precise O(n2) as at most C(n, 2) edges are added from G to G'.
Theorem: G has a Hamiltonian cycle if and only if G' has a TSP tour of cost at most n.
Proof: Split into two parts:
• (if) G' has a TSP tour of cost at most n (YES-instance of TSP) → G has a Hamiltonian cycle (YES-instance of HC)
• (only if) G has a Hamiltonian cycle (YES-instance of HC) → G' has a TSP tour of cost at most n (YES-instance of TSP)
To be added
The key idea (major hint) is to realize that Independent Set and Vertex Cover are related, one set is the complement of the other set.
Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.
X ⊆ V is a vertex cover of G if and only if V-X is an independent set of G.
Take note that this reduction runs in poly-time, in O(V).
It is easy to see that a YES-instance for IS if and only YES-instance for VC.
Proof → and ← are to be added soon.
To be added
To be added
The key idea (major hint) is to that PARTITION has n Integers only but KNAPSACK has n pair of Integers. How about duplicating the Integers? Also PARTITION has a specific target value (half of total of the n Integers) that can also be used as appropriate parameter for KNAPSACK.
Can you work out the details of the poly-time reduction and its proof yourself?
Try first before clicking next.
Given a PARTITION instance α with T = [w1, w2, ..., wn] with total sum S = ∑i=[1..n] wi, construct a KNAPSACK instance β: {(w1, w1), (w2,w2), ..., (wn,wn)}
with capacity W = S/2 and threshold V = S/2.
Take note that this reduction runs in poly-time, to be precise O(n · log (wmax)) as it just copies n weights to n (weight, weight-as-value) pairs. If we assume wmax fits in standard 32/64-bit signed Integers, then log (wmax)) is just 32/64 respectively and this reduction runs in O(n).
Theorem: YES-instance for PARTITION if and only YES-instance for KNAPSACK.
Proof: Split into two parts:
• YES-instance for PARTITION → YES-instance for KNAPSACK.
• YES-instance for KNAPSACK → YES-instance for PARTITION.