Linked List is a data structure consisting of a group of vertices (nodes) which together represent a sequence. Under the simplest form, each vertex is composed of a data and a reference (link) to the next vertex in the sequence. Try clicking for a sample animation on searching a value in a (Singly) Linked List.
Linked List (and its variations) can be used as the underlying data structure to implement List, Stack, Queue, and Deque ADTs (read this Wikipedia article about ADT if you are not familiar with that term). Another potential data structure that can be used to implement List ADT is (resize-able) array.
In this visualization, we discuss (Singly) Linked List (LL) — with a single next pointer — and its two variants: Stack and Queue, and also Doubly Linked List (DLL) — with both next and previous pointers — and its variant: Deque.
We decide to group five related modes involving Linked List (LL, Stack, Queue, DLL, Deque) in one single visualization page. To facilitate more diversity, we randomize the selected mode upon loading this direct URL: https://visualgo.net/en/list.
However, you can use the following URL shortcuts to access individual mode directly (only works for logged-in users who have cleared reading all 3 sectors of these lecture notes):
Linked List data structure is commonly taught in Computer Science (CS) undergraduate courses for a few reasons:
List is a sequence of items/data where positional order matter {a0, a1, ..., aN-2, aN-1}.
Common List ADT operations are:
Discussion 1: What if we want to remove item with specific value v in the list?
Discussion 2: Can a List ADT contains duplicate items, i.e., ai = aj where i ≠ j?
Please review (Compact) Array data structure that can also be used to implement List ADT.
For fixed-size collections with known max limit of number of items that will ever be needed, i.e., the max size of M, then array is already a reasonably good data structure for List ADT implementation.
For variable-size collections with unknown size M and where dynamic operations such as insert/remove are common, a simple (fixed-size) array is actually a poor choice of data structure.
For such applications, there are better data structures, including Linked List. Read on...
We now introduce the Linked List data structure. It uses pointers/references to allow items/data to be non-contiguous in memory (that is the main difference with a simple array). The items are ordered from index 0 to index N-1 by associating item i with its neighbour item i+1 through a pointer.
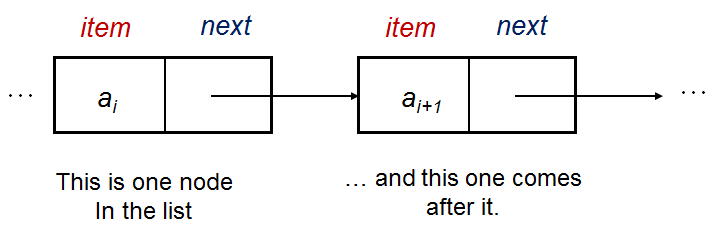
In its basic form, a single vertex (node) in the Linked List has this rough structure:
struct Vertex { // we can use either C struct or C++/Python/Java class
int item; // the data is stored here, an integer in this example
Vertex* next; // this pointer tells us where is the next vertex
};Using the default example Linked List [22 (head)->2->77->6->43->76->89 (tail)] for illustration, we have:
a0 with its item = 22 and its next = a1,
a1 with its item = 2 and its next = a2,
...
a6 with its item = 89 and its next = null.
Discussion: Which one is better for a C++ implementation of Linked List? struct or class? How about Python or Java implementation?
We also have a few additional data that we remember in this Linked List data structure. We use the default example Linked List [22 (head)->2->77->6->43->76->89 (tail)] for illustration.
That's it, we only add three more extra variables in data structure.
Note that there are various subtle differences found in many Computer Science textbooks on how to implement a (Singly) Linked List e.g., use tail pointer or not, circular or not, use dummy head item or not, allow duplicate items or not — see this slide.
Our version in this visualization (with tail pointer, not circular, without dummy head, disallow duplicate) may not be 100% the same compared to what you learn in your class but the basic ideas should remain the same.
In this visualization, each vertex has Integer item, but this can easily be changed to any other data type as needed.
Since we only keep the head and tail pointers, list traversal subroutine is needed to reach positions other than the head (index 0) and the tail (index N-1).
As this sub-routine is so frequently used, we will abstract it out as a function. The code below is written in C++.
Vertex* Get(int i) { // returns the vertex
Vertex* ptr = head; // we have to start from head
for (int k = 0; k < i; ++k) // advance forward i time(s)
ptr = ptr->next; // the pointers are pointing to the higher index
return ptr;
}It runs in O(N) as i can be as big as index N-2.
Compare this with array where we can access index i in O(1) time.
As we only have direct reference to the first head item and the last tail item, plus the pointers are pointing to the right (higher position/index), we can only access the rest by starting from the head item and hopping through the next pointers. On the default [22 (head)->2->77->6->43->76->89 (tail)], we have:
— found in the example above at position/index 2 (0-based indexing).
— not found in the example above, and this is only known after all N items are examined, so Search(v) has O(N) worst case time complexity.
There are more cases than array version due to the nature of Linked List.
Most CS students who learn Linked List for the first time usually are not aware of all cases until they figure it out themselves when their Linked List code fail.
In this e-Lecture, we directly elaborate all cases.
For insert(i, v), there are four (legal) possibilities, i.e., item v is added to:
The (C++) code for insertion at head is simple and efficient, in O(1):
Vertex* vtx = new Vertex(); // create new vertex vtx from item v
vtx->item = v;
vtx->next = head; // link this new vertex to the (old) head vertex
head = vtx; // the new vertex becomes the new head
Try , which is insert(0, 50), on the example Linked List [22 (head)->2->77->6->43->76->89 (tail)].
Discussion: What happen if we use array implementation for insertion at head of the list?
Empty data structure is a common corner/special case that can often cause unexpected crash if not properly tested. It is legal to insert a new item into a currently empty list, i.e., at index i = 0. Fortunately, the same pseudo-code for insertion at head also works for an empty list so we can just use the same code as in this slide (with one minor change, we also need to set tail = head).
Try , which is insert(0, 50), but on the empty Linked List [].
With the Linked List traversal Get(i) sub-routine, we can now implement insertion in the middle of the Linked List as follows (in C++):
Vertex* pre = Get(i-1); // traverse to (i-1)-th vertex, O(N)
aft = pre->next; // aft cannot be null, think about it
Vertex* vtx = new Vertex(); // create new vertex
vtx->item = v;
vtx->next = aft; // link this
pre->next = vtx; // and this
Try on the example Linked List [22 (head)->2->77->6->43->76->89 (tail)].
Also try on the same example Linked List. This is a corner case: Insert at the position of tail item, shifting the tail to one position to its right.
This operation is slow, O(N), due to the need for traversing the list (e.g. if i close to N-1).
If we also remember the tail pointer as with the implementation in this e-Lecture (which is advisable as it is just one additional pointer variable), we can perform insertion beyond the tail item (at i = N) efficiently, in O(1):
Vertex* vtx = new Vertex(); // this is also a C++ code
vtx->item = v; // create new vertex vtx from item v
tail->next = vtx; // just link this, as tail is the i = (N-1)-th item
tail = vtx; // now update the tail pointer
Try , which is insert(7, 10), on the example Linked List [22 (head)->2->77->6->43->76->89 (tail)] . A common misconception is to say that this is insertion at tail. Insertion at tail element is insert(N-1, v). Insertion beyond the tail is insert(N, v).
Discussion: What happen if we use array implementation for insertion beyond the tail of the list?
For remove(i), there are three (legal) possibilities, i.e., index i is:
Discussion: Compare this slide with Insertion Cases slide to realize the subtle differences. Is removing anything from an already empty Linked List considered 'legal'?
This case is straightforward (written in C++):
if (head == NULL) return; // avoid crashing when SLL is empty
Vertex* tmp = head; // so we can delete it later
head = head->next; // book keeping, update the head pointer
delete tmp; // which is the old head
Try repeatedly on the (shorter) example Linked List [22 (head)->2->77->6 (tail)]. It will continuously working correctly up until the Linked List contains one item where the head = the tail item. We prevent execution if the LL is already empty as it is an illegal case.
Discussion: What happen if we use array implementation for removal of head of the list?
With the Linked List traversal Get(i) sub-routine (discussed earlier), we can now implement removal of the middle item of the Linked List as follows (in C++):
Vertex* pre = Get(i-1); // traverse to (i-1)-th vertex, O(N)
Vertex* del = pre->next, aft = del->next;
pre->next = aft; // bypass del
delete del;
Try , the element at index N-2 (as N = 7 in the example [22 (head)->2->77->6->43->76->89 (tail)] .
This is the worst O(N) case on the example above.
Note that Remove(N-1) is removal at tail that requires us to update the tail pointer, see the next case.
We can implement the removal of the tail of the Linked List as follows, assuming that the Linked List has more than 1 item (in C++):
Vertex* pre = head;
tmp = head->next;
while (tmp->next != null) // while my neighbor is not the tail
pre = pre->next, tmp = tmp->next;
pre->next = null;
delete tmp; // tmp = (old) tail
tail = pre; // update tail pointer
Try repeatedly on the (shorter) example Linked List [22 (head)->2->77->6 (tail)]. It will continuously working correctly up until the Linked List contains one item where the head = the tail item and we switch to removal at head case. We prevent execution if the LL is already empty as it is an illegal case.
Actually, if we also maintain the size of the Linked List N (compare with this slide), we can use the Linked List traversal sub-routine Get(i) to implement the removal of the tail of the Linked List this way (in C++):
Vertex* pre = Get(N-2); // go to one index just before tail, O(N)
pre->next = null;
delete tail;
tail = pre; // we have access to old tail
Notice that this operation is slow, O(N), just because of the need to update the tail pointer from item N-1 backwards by one unit to item N-2 so that future insertion after tail remains correct... This deficiency will be later addressed in Doubly Linked List variant.
Discussion: What happen if we use array implementation for removal of tail of the list?
get(i) is slow: O(N).
In Linked List, we need to perform sequential access from head element.
search(v)
In the best case, v is found at the first position, O(1).
In the worst case, v is not found in the list and we require O(N) scan to determine that.
insert(i, v)
In the best case, insert at i = 0 or at i = N, head and tail pointers help, O(1).
In the worst case, insert at i = N-1, we need to find the item N-2 just before the tail, O(N).
remove(i)
In the best case, remove at i = 0, head pointer helps, O(1).
In the worst case, remove at i = N-1, due to the need to update the tail pointer, O(N).
Pure (Singly) Linked List applications are surprisingly rare as the simpler resizeable compact array (vector) can do the job better, compare the Linked List version with the compact array version.
However, the basic concept of Linked List that allows the vertices to be non-contiguous in memory makes it an excellent resize-able data structure for the next two other Abstract Data Types: Stack and Queue.
Stack is a particular kind of Abstract Data Type in which the main operations on the collection are the addition of an item to the collection, known as push, only to the top of the stack and removal of an item, known as pop, only from the top of the stack.
It is known as Last-In-First-Out (LIFO) data structure, e.g., the stack of book below.
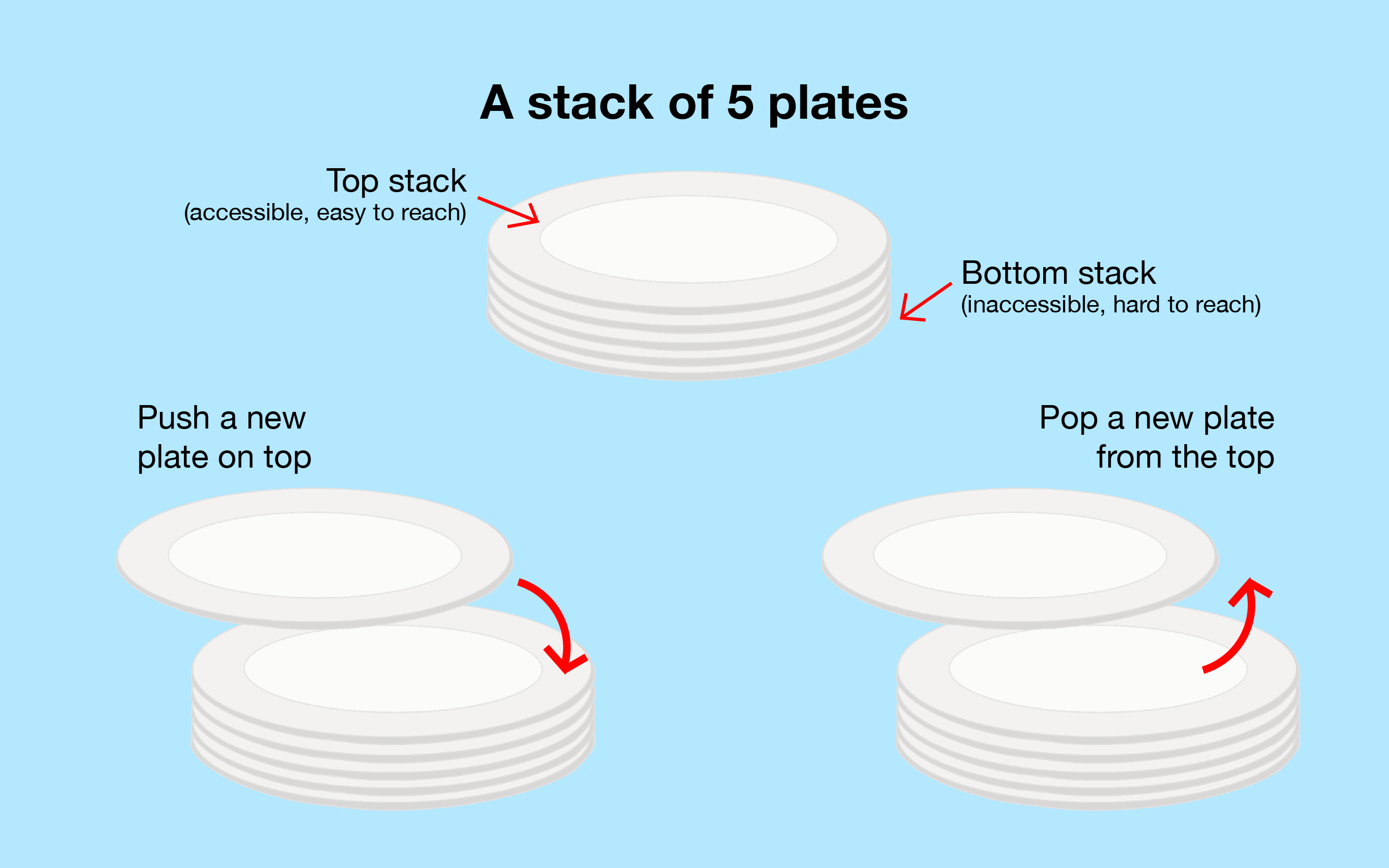
In most implementations and also in this visualization, Stack is basically a protected (Singly) Linked List where we can only peek at the head item, push a new item only to the head (insert at head), e.g., try , and pop existing item only from the head (remove from head), e.g., try . All operations are O(1).
In this visualization, we orientate the (Single) Linked List top down, with the head/tail item at the top/bottom, respectively. In the example, we have [2 (top/head)->7->5->3->1->9 (bottom/tail)]. Due to vertical screen size limit (in landscape mode), we only allow a Stack of at most 7 items in this visualization.
Discussion: Can we use vector, a resizeable array, to implement Stack ADT efficiently?
Stack has a few popular textbook applications. Some examples:
Mathematical expression can get quite convoluted, e.g., {[x+2]^(2+5)-2}*(y+5).
Bracket Matching problem is a problem of checking whether all brackets in the given input are matched correctly, i.e., ( with ), [ with ] and { with }, and so on.
Bracket Matching is equally useful for checking the legality of a source code.
Discussion: It turns out that we can use Stack's LIFO behavior to solve this problem.
The question is how?
Postfix expression is a mathematical expression in: operand1 operand2 operator format which is different from what human is most comfortable at, the Infix expression: operand1 operator operand2.
For example, expression 2 3 + 4 * is the Postfix version of (2+3)*4.
In Postfix expression, we do not need brackets.
Discussion: It turns out that we can also use Stack to solve this problem efficiently.
The question is how?
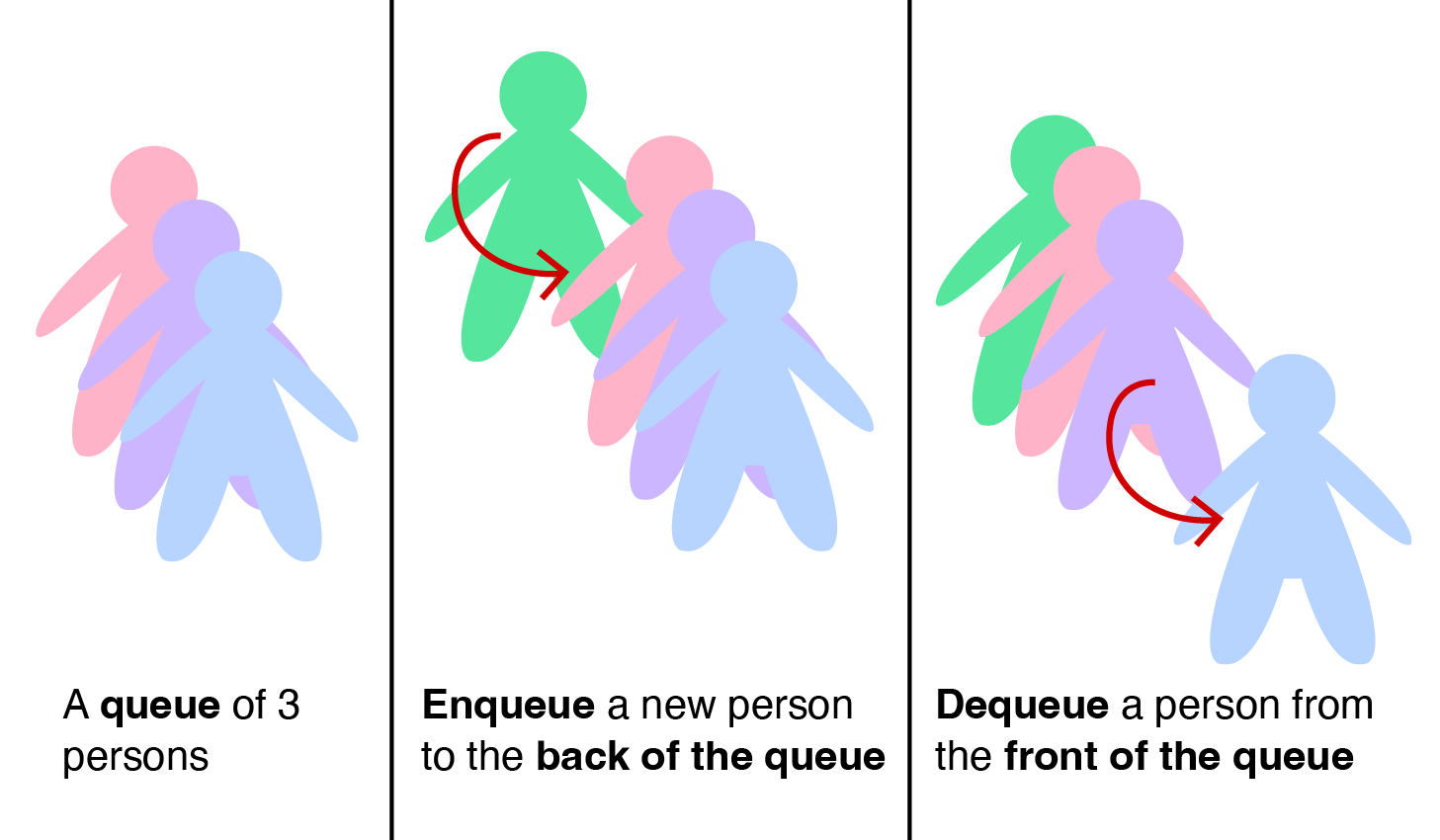
Queue is another Abstract Data Type in which the items in the collection are kept in order and the main operations on the collection are the addition of items to the back position (enqueue) and removal of items from the front position (dequeue).
It is known as First-In-First-Out (FIFO) data structure as the first item to be enqueued will eventually be the first item to be dequeued, as in real life queues (see below).
If we simply use the compact array implementation for this Queue ADT with a0 is the front of the queue and aN-1 is the back of the queue, we will encounter major performance issue with the dequeue operation.
This is because insertion at the back of a compact array is fast, O(1), but removal at the front of a compact array is slow due to the need to shift items, please review this slide.
Another possible array implementation is to avoid that shifting of items during dequeue operation by having two indices: front (the index of the queue front-most item, increased after a dequeue operation) and back (the index of the queue back-most item, also increased after an enqueue operation).
Suppose we use an array of size M = 8 items and the content of our queue is as follows: [(2,4,1,7),-,-,-,-] with front = 0 (underlined) and back = 3 (italic). The current active queue elements are highlighted with (green color).
If we call dequeue(), we have [-,(4,1,7),-,-,-,-], front = 0+1 = 1, and back = 3.
If we call enqueue(5), we have [-,(4,1,7,5),-,-,-], front = 1, and back = 3+1 = 4.
However, many dequeue and enqueue operations later, we may have [-,-,-,-,-,6,2,3], front = 5, and back = 7. By now, we cannot enqueue anything else albeit we have many empty spaces at the front of the array.
If we allow both front and back indices to "wrap back" to index 0 when they have reached index M-1, we effectively make the array "circular" and we can use the empty spaces.
For example, if we call enqueue(8) next, we have [8),-,-,-,-,(6,2,3], front = 5, and back = (7+1)%8 = 0.
Yet, this does not solve the main problem of fixed-size array implementation. A few more enqueue operations later, we may have [8,10,11,12,13),(6,2,3], front = 5, and back = 4. At this point (front = (back+1) % M)), we cannot enqueue anything else.
Do note that if we know that our queue size will never exceed the fixed array size M, then the circular array idea is actually already a good way to implement Queue ADT.
However, if we do not know the upper bound of queue size, we can enlarge (double) the size of the array, e.g., make M = 2*8 = 16 (two-times larger), but that will entail re-copying the items from index front to back in a slow (but rare) O(N) process to have [(6,2,3,8,10,11,12,13),-,-,-,-,-,-,-,-,], front = 0, and back = 7.
PS1: If you understand amortized analysis, this heavy O(N) cost when the circular array is full can actually be spread out so that each enqueue remains O(1) in amortized sense.
PS2: There is an alternative way to implement an efficient Queue using two Stacks. How?
If we do not really know the the upper bound of queue size, then Singly Linked List (SLL) can be a good data structure to implement Queue ADT.
Recall that in a Queue, we only need the two extreme ends of the List, one for insertion (enqueue) only and one for removal (dequeue) only.
If we review this slide, we see that insertion after tail and removal from head in a Singly Linked List are fast, i.e., O(1). Thus, we designate the head/tail of the Singly Linked List as the front/back of the queue, respectively. Then, as the items in a Linked List are not stored contiguously in computer memory, our Linked List can grow and shrink as needed.
In our visualization, Queue is basically a protected Singly Linked List where we can only peek at the head item, enqueue a new item to one position after the current tail, e.g., try , and dequeue existing item from the head, e.g., try (which is essentially a dequeue operation). All operations are O(1).
Queue ADT is usually used to simulate real queues.
One super important application of Queue ADT is inside the Breadth-First Search graph traversal algorithm.
Doubly Linked List (DLL) is 99% the same as its Singly Linked List version. The main difference is that now each vertex contains two pointers. The next pointer is the same as in Singly Linked List version in which it links item ai with the next item ai+1, if exists. The additional prev pointer also links item ai with the previous item ai-1, if exists.
The usage of prev pointers makes it possible to move/iterate backwards at the expense of two-times memory usage requirement as now each vertex records one additional pointer. The positive side effect of this ability to move backwards is now we can address the weak removal at tail case of the Singly Linked List.
In this visualization, notice that the edges in Doubly Linked List (and later Deque) are undirected (bidirectional) edges.
The main problem of removal of the tail element in the Singly Linked List, even if we have direct access to the tail item via the tail pointer, is that we then have to update the tail pointer to point to one item just before the tail after such removal.
With Doubly Linked List ability to move backwards, we can find this item before the tail via tail->prev... Thus, we can implement removal of tail this way (in C++):
Vertex* tmp = tail; // remember tail item
tail = tail->prev; // the key step to achieve O(1) performance :O
tail->next = null; // remove this dangling reference
delete tmp; // remove the old tail
Now this operation is O(1). Try on example DLL [22 (head)<->2<->77<->6<->43<->76<->89 (tail)].
As we have one more pointer prev for each vertex, their values need to be updated too during each insertion or removal. Try all these operations on example DLL [22 (head)<->2<->77<->6<->43<->76<->89 (tail)].
Try — additional step: 22's prev pointer points to new head 50.
Try — additional step: 10's prev pointer points to old tail 89.
Try — additional step: 6's/44's prev pointers point to 44/77, respectively.
Try — set new head 2's prev pointer to null.
Try — set 89's prev pointer to 43.
Double-ended queue (often abbreviated to deque, pronounced deck) is an Abstract Data Type that generalizes a Queue, for which elements can be added to or removed only from either the front (head) or back (tail).
In our visualization, Deque is basically a protected Doubly Linked List where we can only:
search the head/tail item (peek front/back),
insert a new item to the head/tail (try or ), and
remove an existing item from the head/tail (try or ).
All operations are O(1).
Deque are used a few advanced applications, like finding the shortest paths 0/1-weighted graph using modified BFS, on some sliding window techniques, etc.
Create operation is the same for all five modes.
However there are minor differences for the search/insert/remove operations among the five modes.
For Stack, you can only peek/restricted-search, push/restricted-insert, and pop/restricted-remove from the top/head.
For Queue, you can only peek/restricted-search from the front (or sometimes, the back), push/restricted-insert from the back, and pop/restricted-remove from the front.
For Deque, you can peek/restricted-search, enqueue/restricted-insert, dequeue/restricted-remove from both front/back, but not from the middle.
Single (Singly) and Doubly Linked List do not have such restrictions.
We have reached the end of this e-Lecture.
But read ahead for a few extra challenges.
The following are the more advanced insights about Linked List:
C++ STL:
forward_list (a Singly Linked List)
stack
queue
list (a Doubly Linked List)
deque (actually not using Doubly Linked List but another technique, see cppreference)
Java API:
LinkedList (already a Doubly Linked List)
Stack
Queue (actually an interface, usually implemented using LinkedList class)
Deque (actually an interface, usually implemented using LinkedList class)
Python:
list for List/Stack/Queue
deque
OCaml:
List
Stack
Queue
No built-in support for Deque
For a few more interesting questions about this data structure, please practice on Linked List training module.
We also have a few programming problems that somewhat requires the usage of this Linked List, Stack, Queue, or Deque data structure:
UVa 11988 - Broken Keyboard (a.k.a. Beiju Text),
Kattis - backspace, and
Kattis - integerlists.
Try them to consolidate and improve your understanding about this data structure. You are allowed to use C++ STL, Python standard library, or Java API if that simplifies your implementation.